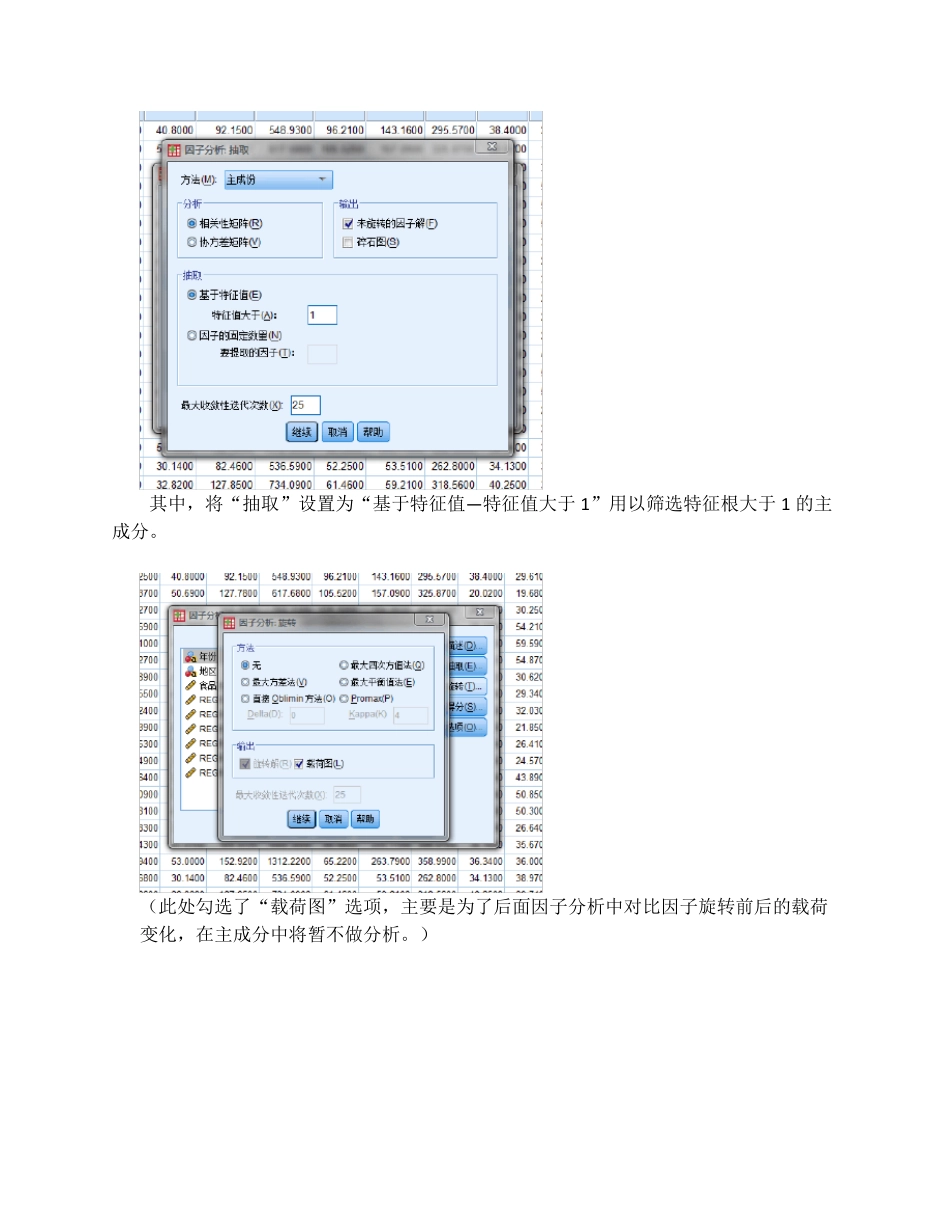
主成分分析 主题描述:中国城镇家庭全年人均食品支出分析。希望通过对原始数据,如粮食支出、肉类支出等多个变量进行主成分分析,研究城镇家庭食品支出的主成分构成,并用较少维度的变量综合表征食品支出这一变量。 模型描述: Y=β1X1+ β2X2+…+ β18X18 其中, 因变量 Y 表示:食品支出总额 自变量 X 包括:X1 粮食支出、X2 淀粉及薯类支出、X3 干豆类支出、X4 油脂类支出、X5 肉禽及制品支出、X6 蛋类支出、X7 水产品支出、X8 菜类支出、X9 调味品支出、X10 糖类支出、X11 烟草类支出、X12 酒和饮料支出、X13 干鲜瓜果类支出、X14糕点类支出、X15 奶及奶制品支出、X16 其他支出、X17 在外用餐支出、X18 食品加工服务费支出共 18 项指标。 数据来源:2007/2008/2009《中国数据统计年鉴》30 个城市自治区居民家庭平均每人全年消费性支出共 93 组数据 (数据见附录) 结果展示及分析: 操作过程:导入数据后,选择“分析”— “降维”— “因子分析”,在弹出的对话框中: 数据选择除“年份”、“城市”、“食品支出”以外的所有变量,“描述”、“抽取”、“得分”选项分别按如下图中设置,其余选项保持默认设置。 其中,将“抽取”设置为“基于特征值— 特征值大于 1”用以筛选特征根大于 1 的主成分。 (此处勾选了“载荷图”选项,主要是为了后面因子分析中对比因子旋转前后的载荷变化,在主成分中将暂不做分析。) 设置“得分”选项是用以计算将原始数据和主成分都进行标准化后的主成分系数。 得到的结果如下: 这是相关系数矩阵,表明各个变量之间的相关性。如果数据在此矩阵中表现出来的相关性较强则可进行主成分分析,否则表明数据不需要做主成分分析。从表中数据看:大多数变量间的相关性中等偏高,个别变量如糕点类与干鲜瓜果类之间的相关性较强… … 说明所选初始变量存在信息上的重叠,可以尝试进行主成分分析。 本表表明所提取主成分的信息。 初始特征值表征的是引入该主成分对原始变量信息的平均解释力度,当主成分的原始特征根大于1 时,表明引入该主成分是有意义的,否则说明引入该主成分对原始变量的解释力度不如引入一个原始变量的解释力度大。从表中可以看出,前六个主成分的“初始特征值均”大于1,被选入作为主成分。 “方差的%” 即“方差贡献率”是用每个主成分的方差除以所有主成分方差的总和,即某一主成分的方差在全部方差中的比重,表明某一主成分综合原始变...