习题集02数字信号处理习题答案VIP免费

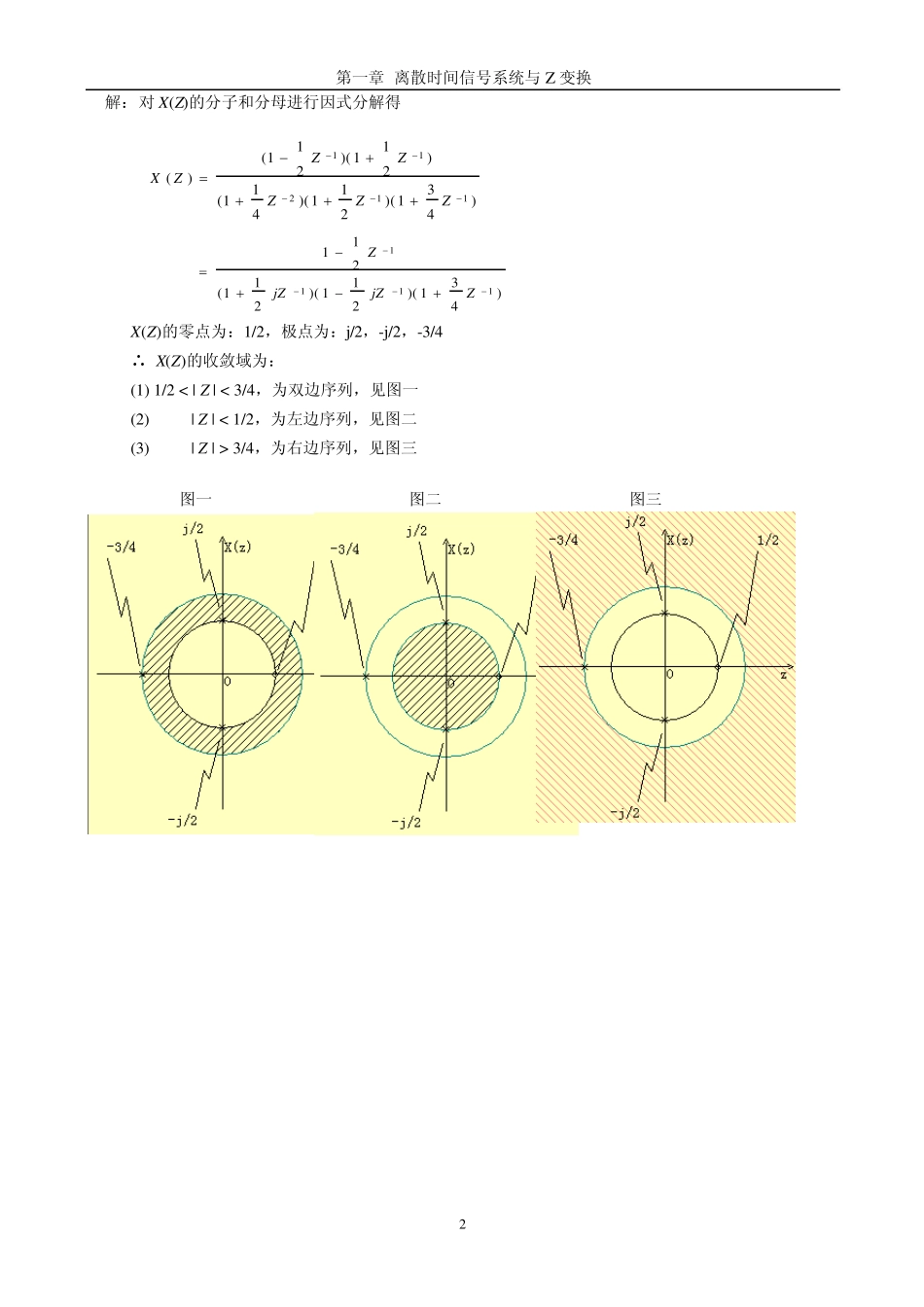
第一章 离散时间信号系统与Z 变换 1 § Z变换  Z变换的定义及收敛域 【习题】 1. 假如)(nx的 z变换代数表示式是下式，问)( zX可能有多少不同的收敛域。 )83451)(411(411)(2122zzzzzX 【分析】 ）要单独讨论，（环状、圆外、圆内：有三种收敛域：双边序列的收敛域为：特殊情况有：左边序列的收敛域为：因果序列的收敛域为：右边序列的收敛域为：特殊情况有：有限长序列的收敛域为 0 0 , , 0 0 , , 0 , 0 0 , 0 , 0 22112121zzRzRnnRznnRznnzRnnzRnznznnnzxxxxxx 第一章 离散时间信号系统与Z 变换 2 解：对X(Z)的分子和分母进行因式分解得 )431)(211)(211(2111111ZjZjZZ X(Z)的零点为：1/2，极点为：j/2，-j/2，-3/4 ∴ X(Z)的收敛域为： (1) 1/2 < | Z | < 3/4，为双边序列，见图一 (2) | Z | < 1/2，为左边序列，见图二 (3) | Z | > 3/4，为右边序列，见图三 图一 图二 图三 )431)(211)(411()211)(211()(11211ZZZZZZX第一章 离散时间信号系统与Z 变换 3  Z反变换 【习题】 2. 有一右边序列 )(nx，其 z 变换为)1)(211(1)(11zzzX (a) 将上式作部分分式展开(用 1z表示)，由展开式求 )(nx 。 (b) 将上式表示成 z 的多项式之比，再作部分分式展开，由展开式求 )(nx ,并说明所得到的序列与(a)所得的是一样的。 【注意】不管哪种表示法最后求出 x(n) 应该是相同的。 解：(a) 因为11122111)(zzzX 且 x(n)是右边序列 所以 )()212()(nunxn (b) 1221211 )1)(21(21231 )1)(21()(2zzzzzzzzzX )()212( )1(2)1(21)()( nunununnxnn 则 第一章 离散时间信号系统与Z 变换 4  Z变换的基本性质和定理 【习题】 3. 对因果序列，初值定理是)(lim)0(zXxz，如果序列为 0n时 0)(nx，问相应的定理是什么？)( nx讨论一个序列，其z变换为： 值。试求其的收敛域包括单位圆， )0( )(xzX 【分析】 这道题讨论如何由双边序列Z变换)( zX来求序列初值)0(x，把序列分成因果序列和反因果序列两部分，〖它们各自由)( zX求)0(x表达式是不同的〗，将它们各自的)0(x相加即得所...