常用玻璃量器示值误差测量不确定度评定VIP免费

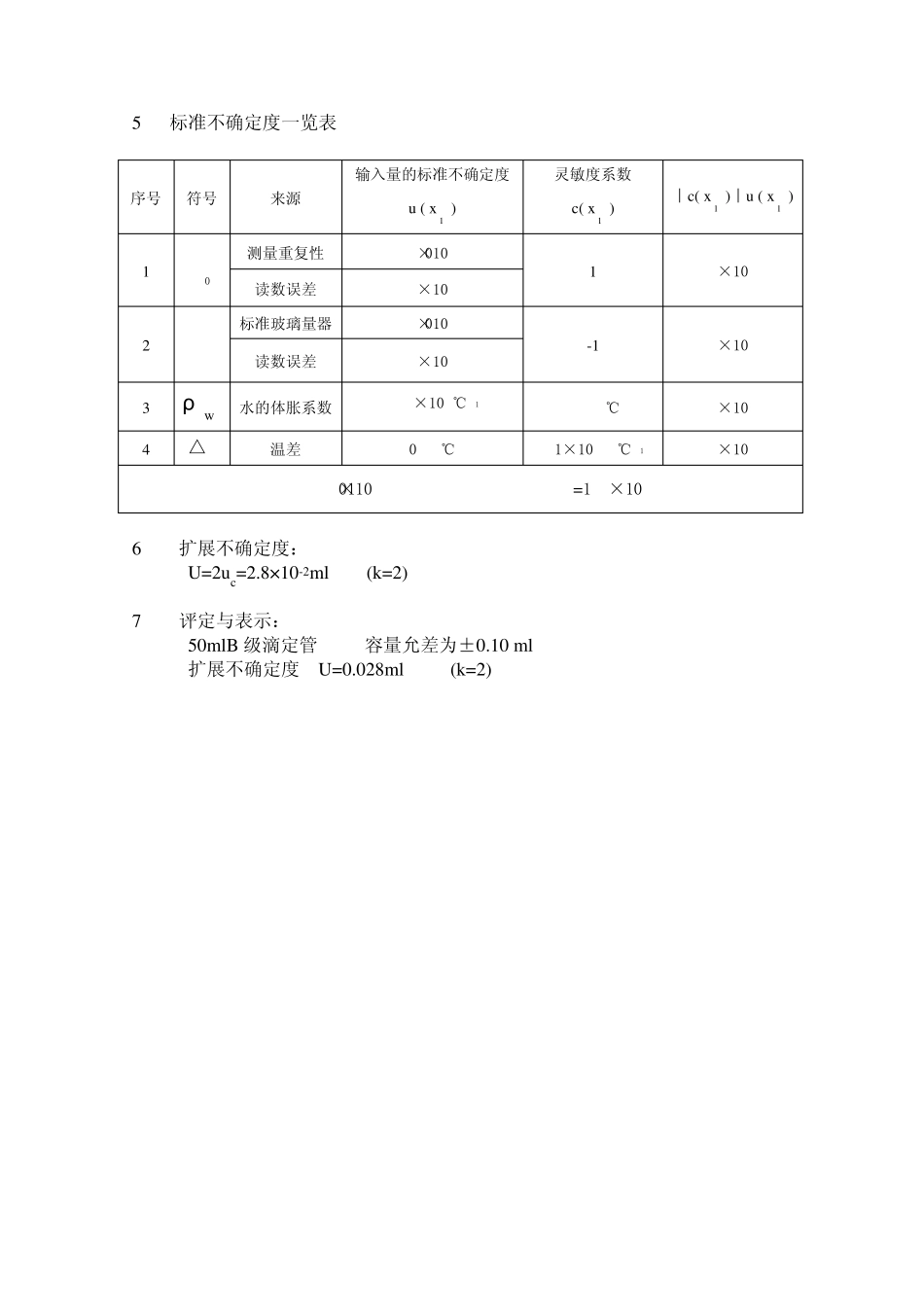
一 常用玻璃量器示值误差测量不确定度评定 （容量比较法） 1、概述 依据常用玻璃量器检定规程，采用容量比较法检定。主标准器为相应规格的标准玻璃量器，其容量允差为被检量器允差的1/5，工作室环境温度20±5℃，室内温度变化不大于 1℃/h,水温与室温之差不超过2℃ 本实例用容量比较法检定50ml B 级滴定管，测量点为0~50ml，t=23℃， β W=2×10-4℃-1 ，△t=0.5℃ 2、数学模型 △V=V0－V20=V0－VB[1+β W△t] 式中：V0 —— 被检量器的标称容量，ml； VB —— 标准玻璃量器的容量，ml; β W —— 水的体胀系数，1/ ℃； △ t —— 标准与被检量器内水的温差，℃。 3、方差和灵敏度系数 uc2=c2(v0)u2(v0)+c2(vB)u2(vB)+c2(βW)u2(βW)+c2(△t)u2(△t) 式中：c（v0）=1 c（vB）=-1 c（β W）=-vB△t=-25ml·℃ c（△t）=-vBβ W=-1×10-2ml·℃-1 4、输入量的标准不确定度 4.1 被检量器测量引入的不确定度u(v0) 4.1.1 测量重复性 对 0~50ml 点重复测量6 次，其最大值与最小值之差R=0.02ml 采用极差法：dn=2.53 u1(v0)= 53.202.0 =8.0×10-3ml 4.1.2 估读误差 估读误差为最小分度的1/10，为0.01ml。 均匀分布，3k u2(v0)= 301.0 =5.8×10-3ml 4.2 标准玻璃量器检定装置引入的不确定度u(vB) 4.2.1 标准玻璃量器 标准玻璃量器的允差为被检量器允差的1/5，为0.02ml 正态分布 ， k=2.58 u1(vB)= 58.202.0 =8.0×10-3ml 4.2.2 检定装置的影响：50ml 滴定管检定装置的影响量为0.01ml 均匀分布，3k u2(vB)= 301.0 =5.8×10-3ml 4.3 水的体胀系数引入的不确定度u(β W) 水的平均体胀系数为2×10-4℃-1，变化量为5×10-5℃-1 均匀分布，3k u(β W)= 31055 =2.9×10-5℃-1 4.4 温差引入的不确定度u(△t) 标准与被检量器温差为△t=0.5℃ 均匀分布， 3k u(△t)= 35.0 =0.29℃ 5 标准不确定度一览表 序号 符号 来源 输入量的标准不确定度 u ( x1 ) 灵敏度系数 c( x1 ) ︱c( x1 )︱u ( x1 ) 1 V0 测量重复性 8.0×10-3ml 1 9.8×10-3ml 读数误差 5.8×10-3ml 2 VB 标准玻璃量器 8.0×10-3ml -1 9.8×10-3ml 读数误差 5.8×10-3ml 3 ρ w 水的体胀系数 2.9×10-5℃-1 -25ml℃ 7.2×10-4ml 4 △t 温差 0.29℃ -1×10-2ml℃-1 2.9×10-3ml uc2=201×10-6ml uc=1.4×10-2ml 6 扩展不确定度： U=2uc=2...