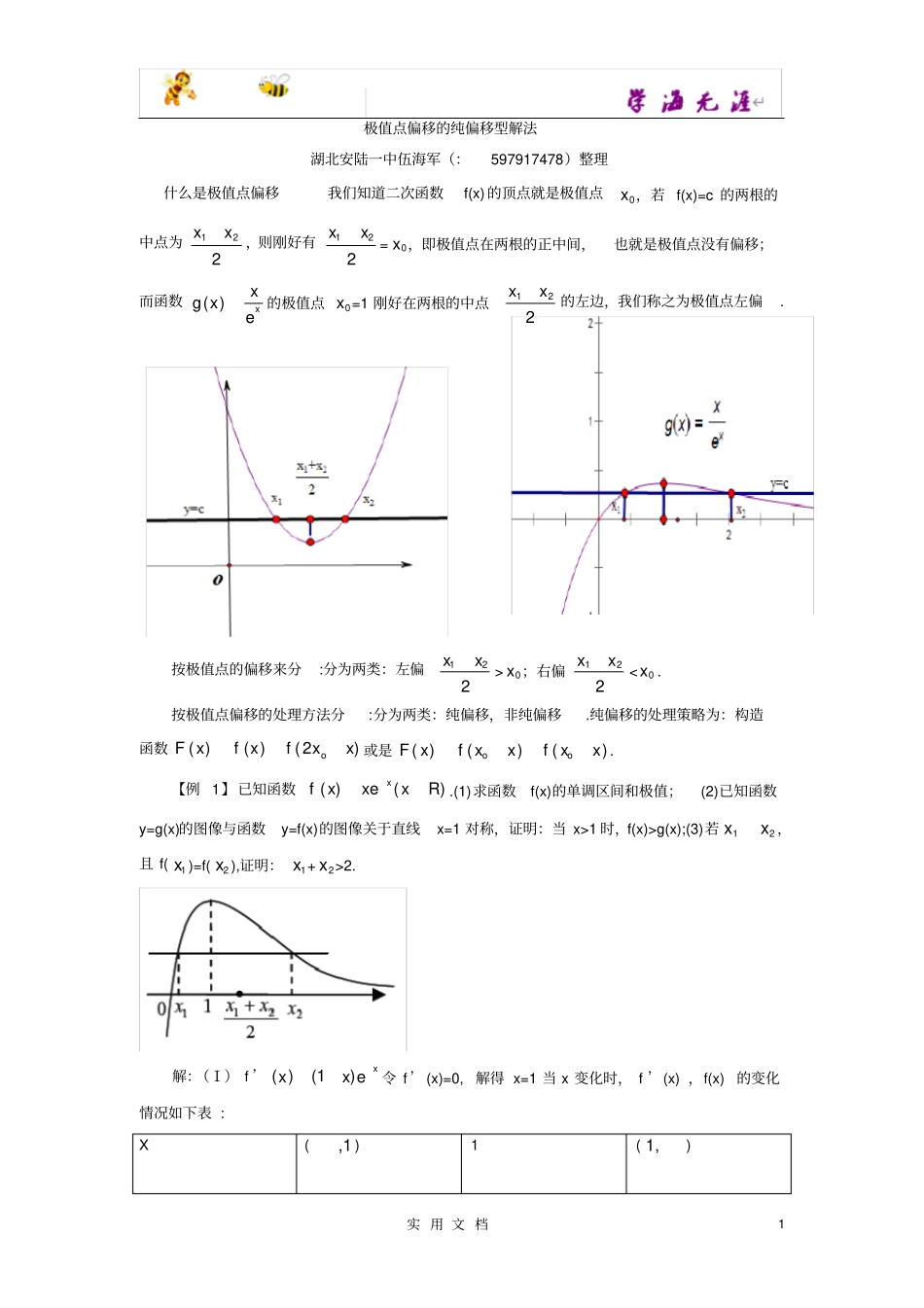
实 用 文 档1 极值点偏移的纯偏移型解法湖北安陆一中伍海军(:597917478)整理什么是极值点偏移我们知道二次函数f(x) 的顶点就是极值点0x ,若 f(x)=c 的两根的中点为221xx,则刚好有221xx=0x ,即极值点在两根的正中间,也就是极值点没有偏移;而函数xexxg)(的极值点0x =1 刚好在两根的中点221xx的左边,我们称之为极值点左偏. 按极值点的偏移来分:分为两类:左偏221xx>0x ;右偏221xx<0x .按极值点偏移的处理方法分:分为两类:纯偏移,非纯偏移.纯偏移的处理策略为:构造函数)2()()(xxfxfxFo或是( )()()ooF xf xxf xx .【例 1】已知函数)()(Rxxexfx.(1)求函数f(x)的单调区间和极值;(2)已知函数y=g(x)的图像与函数y=f(x)的图像关于直线x=1 对称,证明:当 x>1 时,f(x)>g(x);(3)若1x2x ,且 f(1x )=f(2x ),证明:1x +2x >2. 解:(Ⅰ) f ’ ( )(1)xxx e令 f ’(x)=0,解得 x=1 当 x 变化时, f ’(x) ,f(x)的变化情况如下表 : X (,1 ) 1 ( 1,) 实 用 文 档2 f ’(x) + 0 - f(x) Z极大值]所以 f(x) 在 (,1) 内是增函数,在( 1,) 内是减函数 .函数 f(x) 在 x=1 处取得极大值f(1) 且 f(1)=1e(Ⅱ)证明:由题意可知g(x)=f(2-x),得 g(x)=(2-x)2xe;令F(x)=f(x)-g(x),即2( )(2)xxF xxexe;于是22'( )(1)(1)xxFxxee;当x>1 时, 2x-2>0, 从而2x-2e10,0,Fxe又所以’(x)>0,从而函数 F( x)在 [1,+ ∞) 是增函数 . 又 F(1)=-1-1ee0,所以 x>1时,有 F(x)>F(1)=0,即 f(x)>g(x). ( Ⅲ) 证明:(1)若121212.(1)(1)0,)),1.xxxxxx12由( )及 f(xf(x则与矛盾(2)若121212(1)(1)0,)),..xxxxxx12由( )及 f(xf(x得与矛盾根据( 1)(2)得1212(1)(1)0,1,1.xxxx不妨设由 ( Ⅱ ) 可 知 ,)2f(x>)2g(x, 则)2g(x=)2f(2-x, 所 以)2f(x>)2f(2-x, 从 而)1f(x>)2f(2-x. 因为21x,所以221x,又由(Ⅰ)可知函数f(x)在区间( - ∞, 1)内事增函数,所以1x >22x , 即12xx >2. 【练习 1】已知函数xaaxxxf)2(ln)(2.(1)讨论)(xf的单调性;(2)设0a,证明:当ax10时,)1()1(xafxaf;(3)若函数)( xfy的图像与 x 轴交于 A,B两点,线段AB 中点的横坐标为x0,证明:f(x0)< 0.解:(I)( )(0,),f x 的定义域为1(21)(1)( )2(2).xaxfxaxaxx(i)若0,( )0,( )(0,)afxf x则所以在单调增加 . (ii )若10,( )0,afxxa则...