2020高考热点等差数列、等比数列题型归纳VIP免费

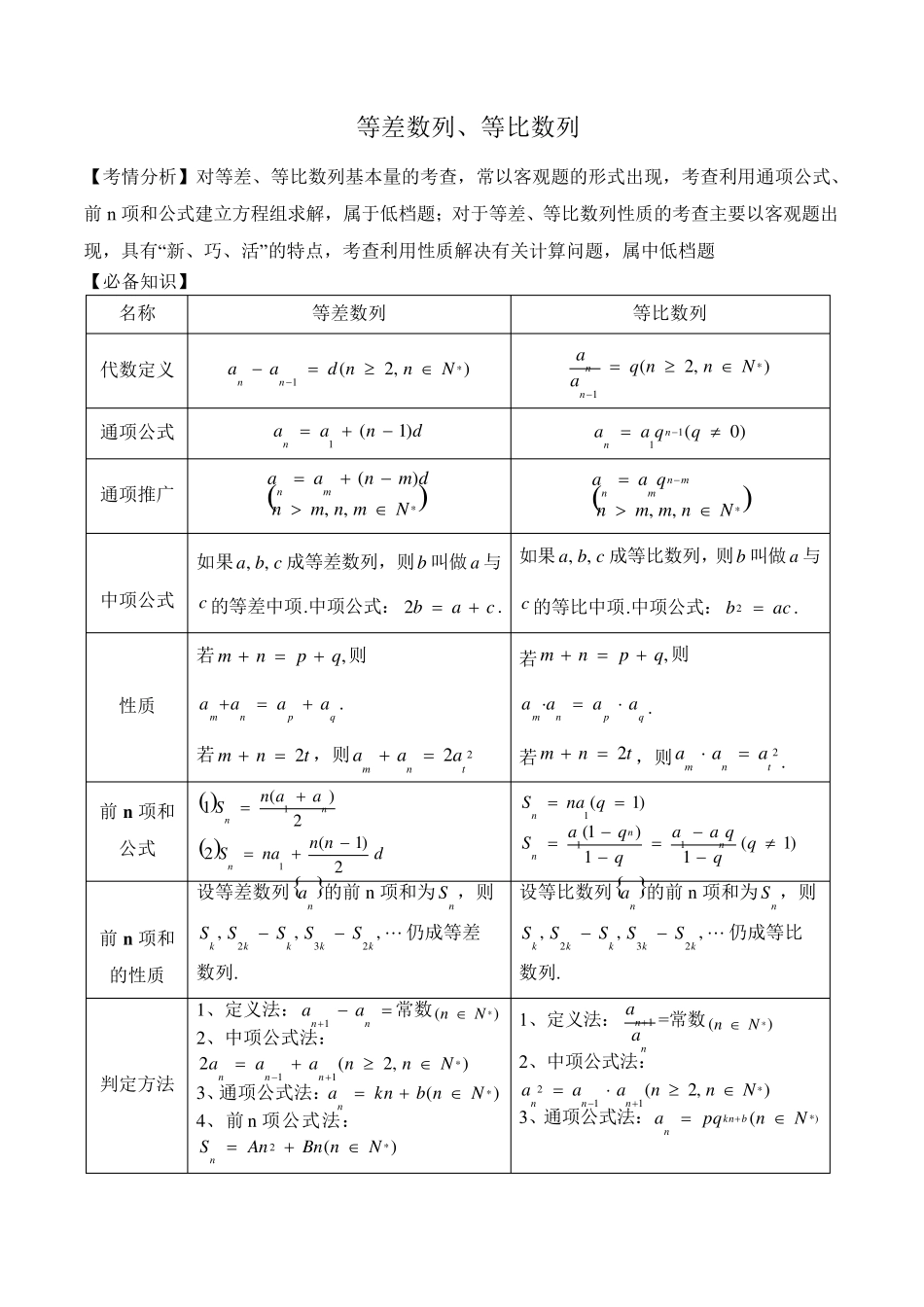
等差数列、等比数列 【考情分析】对等差、等比数列基本量的考查，常以客观题的形式出现，考查利用通项公式、前 n 项和公式建立方程组求解，属于低档题；对于等差、等比数列性质的考查主要以客观题出现，具有“新、巧、活”的特点，考查利用性质解决有关计算问题，属中低档题 【必备知识】 名称 等差数列 等比数列 代数定义 ),2(*1Nnndaann ),2(*1Nnnqaann 通项公式 dnaan)1(1 )0(11 qqaann 通项推广 *,,)(Nmnmndmnaamn *,,Nnmmnqaamnmn 中项公式 如果cba,,成等差数列，则b 叫做 a 与c 的等差中项.中项公式：cab2. 如果cba,,成等比数列，则b 叫做 a 与c 的等比中项.中项公式：acb2. 性质 若,qpnm则qpnmaaaa. 若tnm2，则22tnmaaa 若,qpnm则qpnmaaaa. 若tnm2，则2tnmaaa. 前 n 项和 公式   dnnnaSaanSnnn2)1(22)(111 )1(11)1()1(111qqqaaqqaSqnaSnnnn 前 n 项和的性质 设等差数列 na的前 n 项和为nS ，则,,,232kkkkkSSSSS仍成等差 数列. 设等比数列 na的前 n 项和为nS ，则,,,232kkkkkSSSSS仍成等比数列. 判定方法 1 、定义法：nnaa1常数 )(*Nn  2 、中项公式法： ),2(2*11Nnnaaannn 3 、通项公式法：)(*Nnbknan 4 、前 n 项公式法：)(*2NnBnAnSn 1、定义法：nnaa1 =常数 )(*Nn  2、中项公式法：),2(*112Nnnaaannn 3、通项公式法：*)(Nnpqabknn 考点一 等差、等比数列基本量的计算 【典型例题】 【例 1】（1）在等差数列 na中，14,2162aa，若 na的前 k 项和为 50，则 k= . （2）已知数列 na为等比数列，21551 aa，前四项的和54S，则4a = . 求等差（比）数列基本量的解题思路： （1）设基本量：首项1a 和公差d（公比 q）； （2）列、解方程（组）：把条件转化为关于1a 和 d（或 q）的方程（组），然后求解，注意整体计算，以减少运算量. 注：等差、等比数列基本量的运算是数列中的一类基本问题,有五个基本量:1a ,)(qd 或，n，na ，nS ，一般可以“知三求二”,通过列方程(组)便可迎刃而解. 【类比训练】（1）已知等差数列 na满足10,45342aaaa，则它的前 10 项的和S10=...