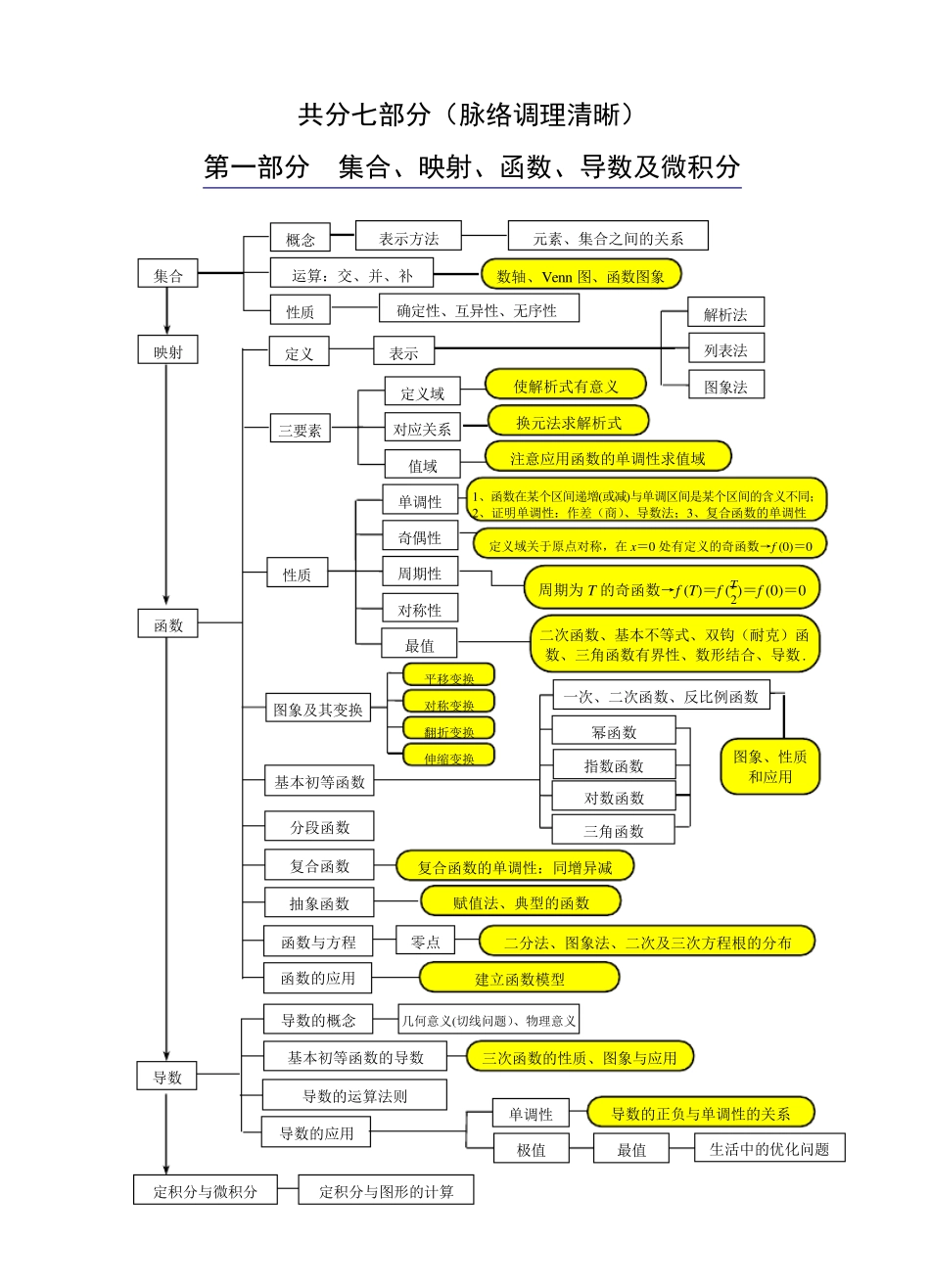
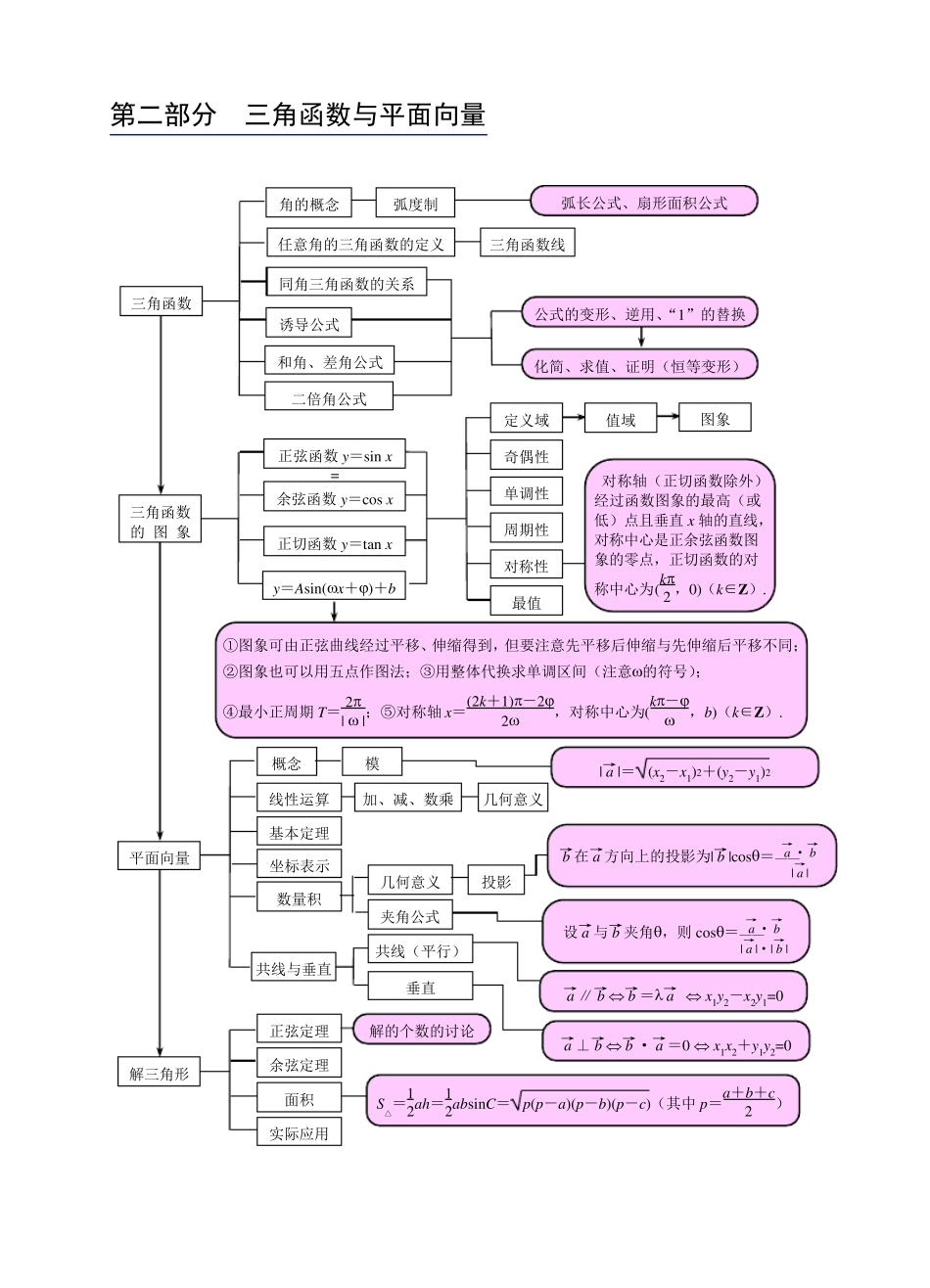
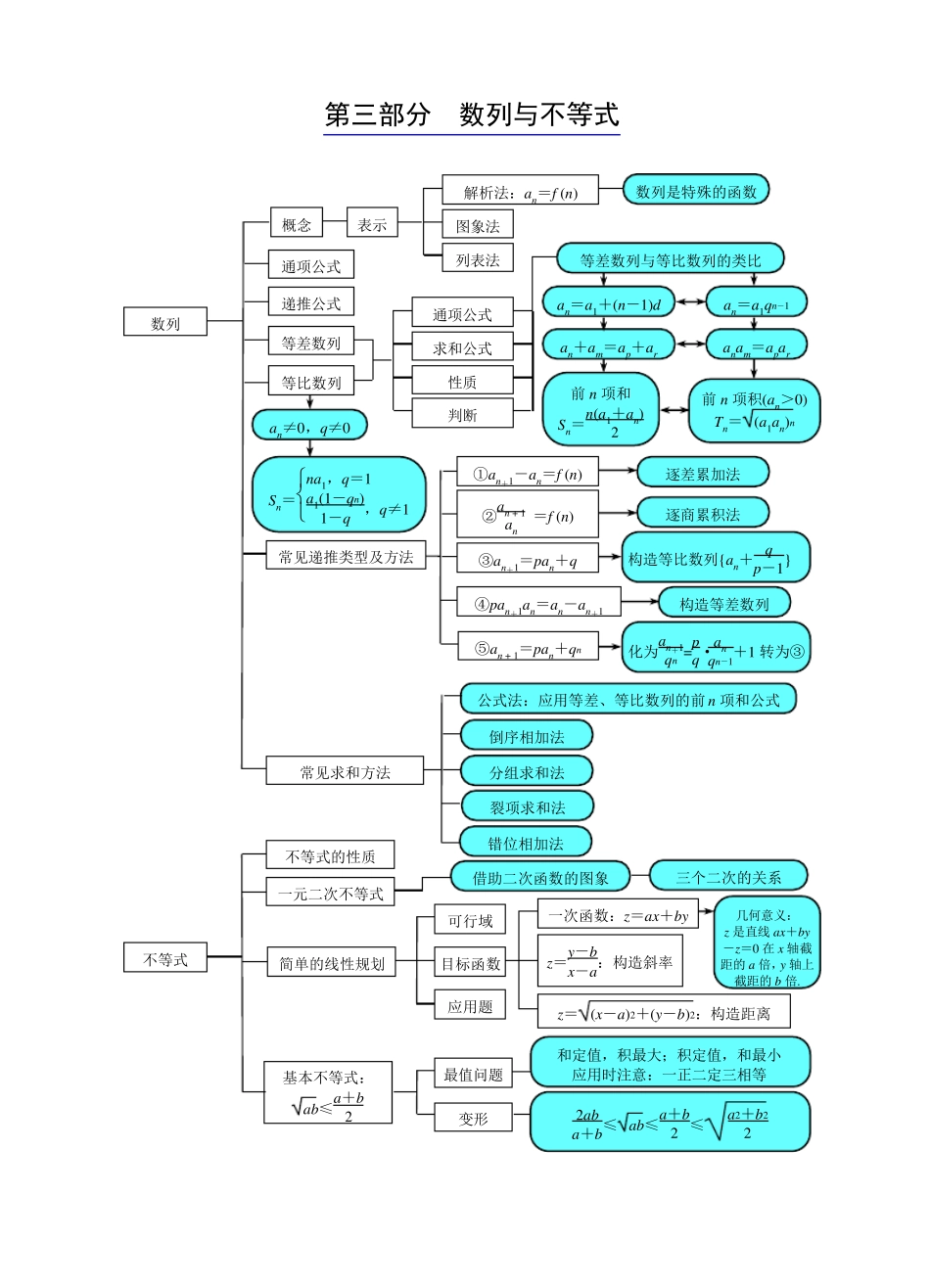
共分七部分(脉络调理清晰) 第一部分 集合、映射、函数、导数及微积分 集合 映射 概念 元素、集合之间的关系 运算:交、并、补 数轴、Venn 图、函数图象 性质 确定性、互异性、无序性 定义 表示 解析法 列表法 三要素 图象法 定义域 对应关系 值域 性质 奇偶性 周期性 对称性 单调性 定义域关于原点对称,在x =0 处有定义的奇函数→f (0)=0 1、函数在某个区间递增(或减)与单调区间是某个区间的含义不同;2、证明单调性:作差(商)、导数法;3、复合函数的单调性 最值 二次函数、基本不等式、双钩(耐克)函数、三角函数有界性、数形结合、导数. 幂函数 对数函数 三角函数基本初等函数 抽象函数 复合函数 赋值法、典型的函数 函数与方程 二分法、图象法、二次及三次方程根的分布 零点 函数的应用 建立函数模型 使解析式有意义 导数 函数 基本初等函数的导数 导数的概念 导数的运算法则 导数的应用 表示方法 换元法求解析式 分段函数 几何意义(切线问题)、物理意义 单调性 导数的正负与单调性的关系 生活中的优化问题 定积分与微积分 定积分与图形的计算 注意应用函数的单调性求值域 周期为 T 的奇函数→f (T)=f (T2)=f (0)=0 复合函数的单调性:同增异减 三次函数的性质、图象与应用 一次、二次函数、反比例函数 指数函数 图象、性质 和应用 平移变换 对称变换 翻折变换 伸缩变换 图象及其变换 最值 极值 第二部分 三角函数与平面向量 角 的 概 念 任 意 角 的 三 角 函 数 的 定 义 三 角 函 数 弧 度 制 弧 长 公 式 、 扇 形 面 积 公 式 三 角 函 数 线 同 角 三 角 函 数 的 关 系 诱 导 公 式 和 角 、 差 角 公 式 二 倍 角 公 式 公 式 的 变 形 、 逆 用 、“ 1” 的 替 换 化 简 、 求 值 、 证 明 ( 恒 等 变 形 ) 三 角 函 数 的 图 象 定 义 域 奇 偶 性 单 调 性 周 期 性 最 值 对 称 轴 ( 正 切 函 数 除 外 )经 过 函 数 图 象 的 最 高 ( 或低 ) 点 且 垂 直 x 轴 的 直 线 ,对 称 中 心 是 正 余 弦 函 数 图象 的 零 点 , 正 切 函 数 的 对称 中 心 为 (k2 , 0)( k∈ Z) . 正 弦 函 数 y= sin x = 余 弦 函 数 y= c...