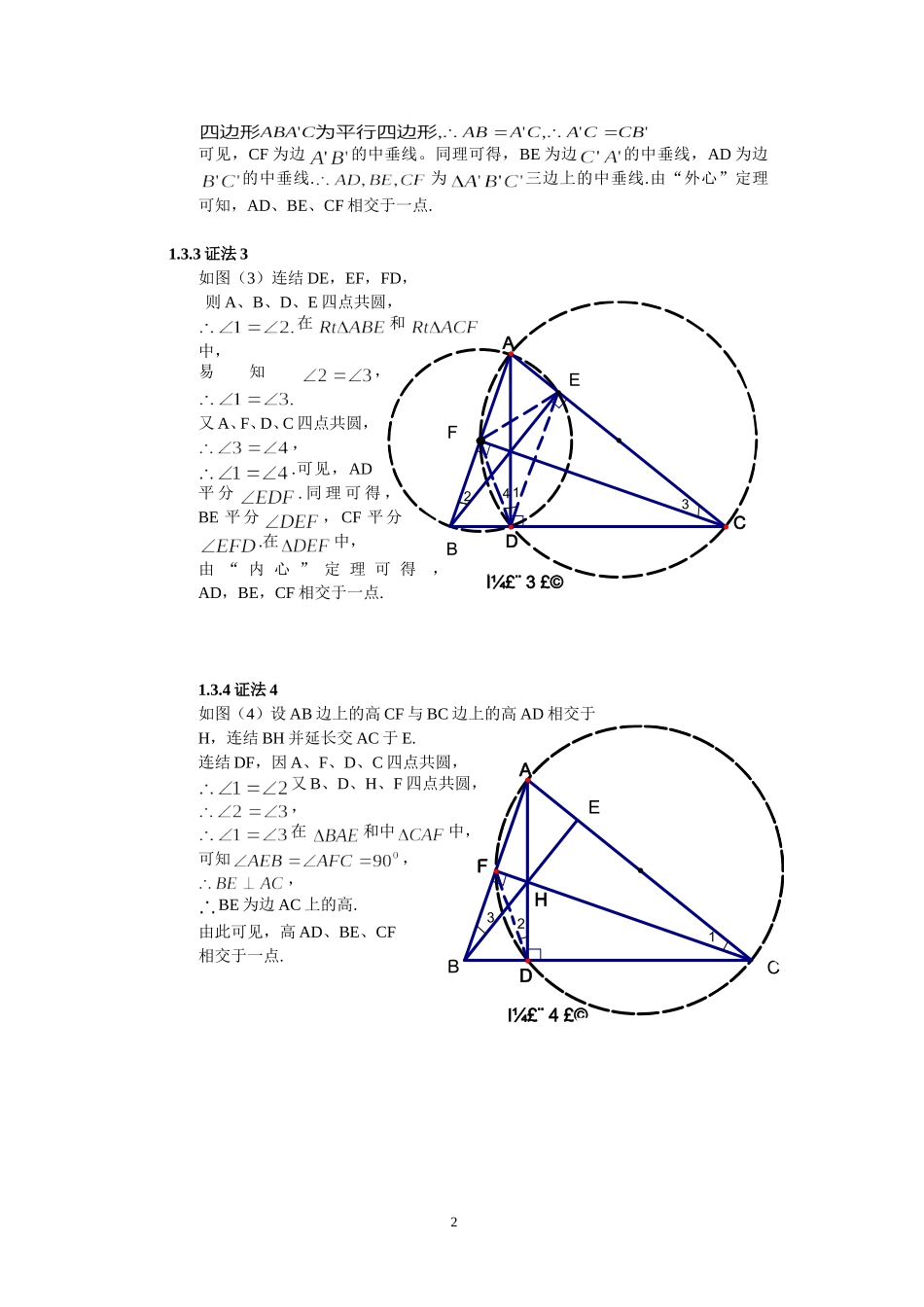
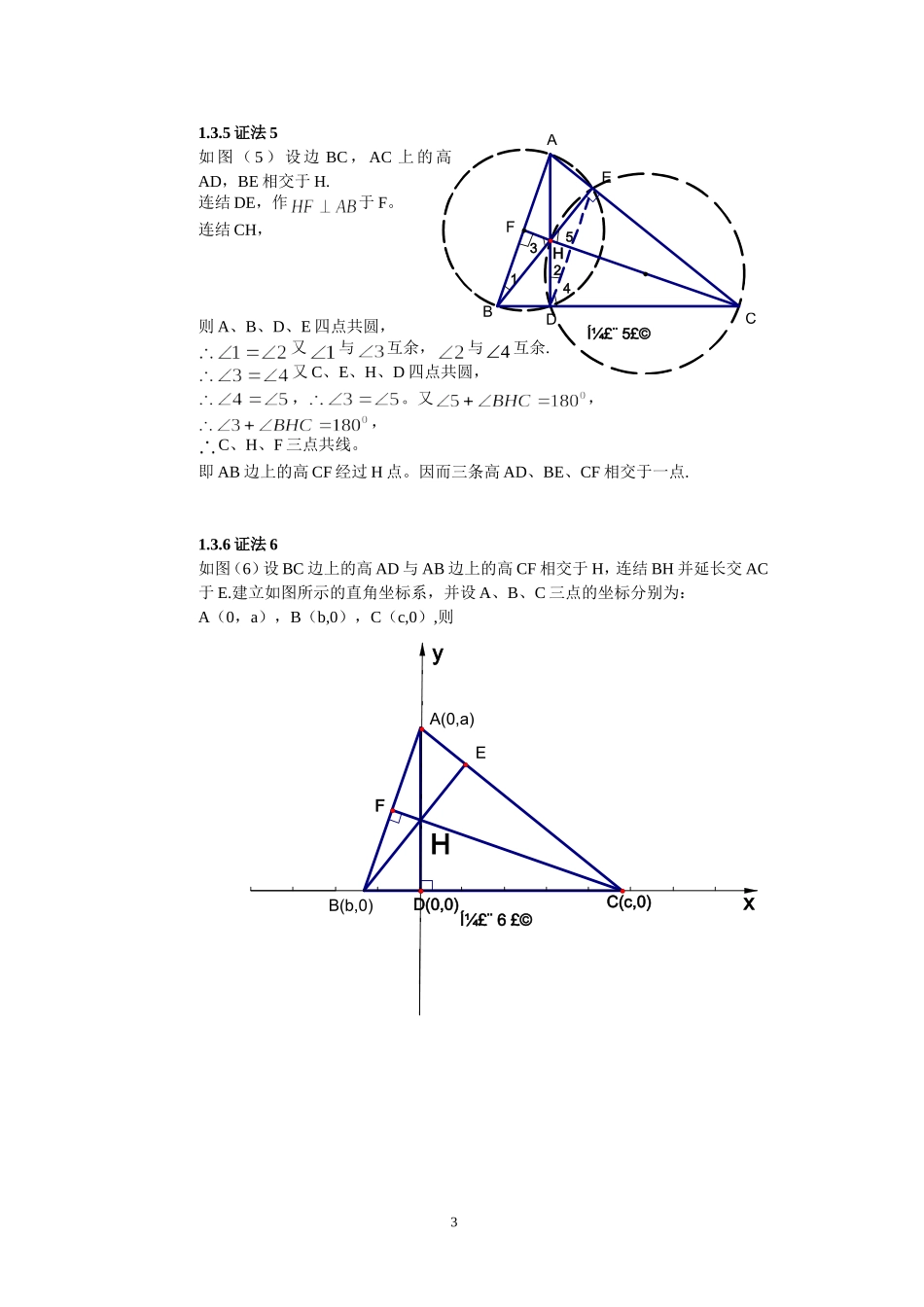
B'A'C'DFEͼ£¨ 2 £©BCAFEDCBAͼ£¨ 1 £©三角形“垂心”定理的 7 种证法 三角形“垂心”定理的证法1.1 定理: 三角形三条高相交于一点,这点叫做三角形的垂心(该定理俗称三角形“垂心”定理). 已知,如图(1)中,AD,BE,CF分别是边 BC,CA,AB 上的高. 求证: AD,BE,CF 相交于一点 1.2 预备定理: 1.塞瓦(Ceva)定理:设 D、E、F 分别是三边 BC、CA、AB 上的点,若,则 AD,BE,CF 交于一点.2.三角形“外心”定理:三角形三边的中垂线相交于一点,此点与三顶点等距,这点叫做三角形的外心.3. 三角形“内心”定理:三角形三内角平分线交于一点,此点与三边等距,这点叫做三角形的内心.1.3 定理的证法 1.3.1 证法 1 如图(1),由已知可得,∽∽,∽三式相乘得:由塞瓦定理可得 AD,BE,CF 相交于一点.1.3.2 证法 2如图(2)分别过A、B、C 做它们所在高的垂线,使之相交成.则同理,13142FEBͼ£¨ 3 £©DCAH123ECBͼ£¨ 4 £©FDA可见,CF 为边的中垂线。同理可得,BE 为边的中垂线,AD 为边的中垂线.为三边上的中垂线.由“外心”定理可知,AD、BE、CF 相交于一点. 1.3.3 证法 3如图(3)连结 DE,EF,FD,则 A、B、D、E 四点共圆,在和中,易知,又 A、F、D、C 四点共圆,,.可见,AD平 分. 同 理 可 得 ,BE 平分,CF 平分.在中,由 “ 内 心 ” 定 理 可 得,AD,BE,CF 相交于一点.1.3.4 证法 4如图(4)设 AB 边上的高 CF 与 BC 边上的高 AD 相交于H,连结 BH 并延长交 AC 于 E.连结 DF,因 A、F、D、C 四点共圆,又 B、D、H、F 四点共圆,,在 和中中,可知,,BE 为边 AC 上的高.由此可见,高 AD、BE、CF相交于一点.254321FEDCBAͼ£¨ 5£©H1.3.5 证法 5如 图 ( 5 ) 设 边 BC , AC 上 的 高AD,BE 相交于 H.连结 DE,作于 F。连结 CH,则 A、B、D、E 四点共圆,又与互余,与4 互余.又 C、E、H、D 四点共圆,,。又,,C、H、F 三点共线。即 AB 边上的高 CF 经过 H 点。因而三条高 AD、BE、CF 相交于一点.1.3.6 证法 6如图(6)设 BC 边上的高 AD 与 AB 边上的高 CF 相交于 H,连结 BH 并延长交 AC于 E.建立如图所示的直角坐标系,并设 A、B、C 三点的坐标分别为:A(0,a),B(b,0),C(c,0),则xyEB(b,0)A(0,a)ͼ£¨ 6 £©FD(0,0)C(c,0)3H即 BE 为 AC 边上的高。...