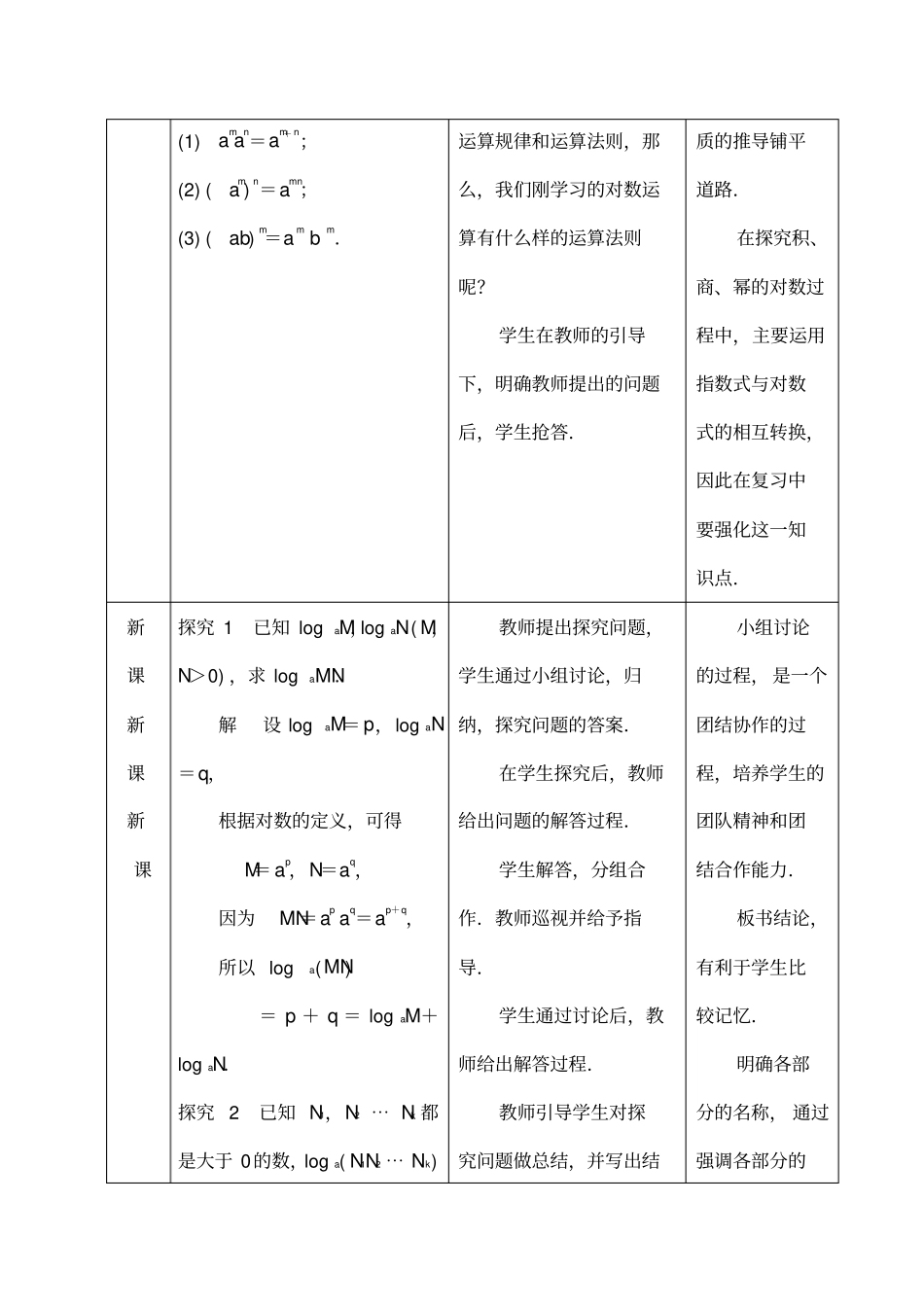
4.2.2 积、商、幂的对数【教学目标】1. 掌握积、商、幂的对数运算法则,并会进行有关运算.2. 培养学生的观察,分析,归纳等逻辑思维能力.3.培养学生勇于发现、勇于探索、勇于创新的精神;培养合作交流等良好品质.【教学重点】积、商、幂的对数运算法则的应用.【教学难点】积、商、幂的对数运算法则的推导.【教学方法】本节教学采用引导发现式教学方法,并充分利用多媒体辅助教学,体现“教师为主导、学生为主体”的教学原则.通过教师在教学过程中的点拨启发,使学生主动思考.通过分组合作的教学方式,使学生在合作中快乐学习, 培养学生的团结协作能力和集体主义情操.通过设置三组“低台阶,小坡度”的练习,满足各层次学生的学习需求,从而培养学生的计算能力和学习数学的兴趣.【教学过程】环节教学内容师生互动设计意图导入1.指数式与对数式的关系:若指数式ab= N,则 logaN=b.2.指数幂的运算法则师:以前,我们学习过数的加、减、乘、除、乘方、开方,数的加减乘除乘方开方都有自己的通过学生抢答,使全体学生回顾有关旧知识,为对数性(1) aman=am+ n;(2) (am)n=amn;(3) (ab)m=a m b m.运算规律和运算法则,那么,我们刚学习的对数运算有什么样的运算法则呢?学生在教师的引导下,明确教师提出的问题后,学生抢答.质的推导铺平道路.在探究积、商、幂的对数过程中,主要运用指数式与对数式的相互转换,因此在复习中要强化这一知识点.新课新课新课探究 1 已知 logaM,log aN ( M,N>0) ,求 logaMN.解设 logaM= p,log aN=q,根据对数的定义,可得M= ap,N=aq,因为MN=ap aq=ap+q,所以 loga(MN) = p + q = log aM+log aN.探究 2 已知 N1,N2 ⋯ Nk 都是大于 0的数,log a( N1N2 ⋯ Nk)教师提出探究问题,学生通过小组讨论,归纳,探究问题的答案.在学生探究后,教师给出问题的解答过程.学生解答,分组合作.教师巡视并给予指导.学生通过讨论后,教师给出解答过程.教师引导学生对探究问题做总结,并写出结小组讨论的过程, 是一个团结协作的过程,培养学生的团队精神和团结合作能力.板书结论,有利于学生比较记忆.明确各部分的名称, 通过强调各部分的等于什么?结论:log a( N1N2⋯ Nk) = log aN1 + log aN2 + ⋯ +log aNk.探究 3 已知 logaM,log aN ( M,N>0) .求 loga MN.解设 logaM= p,log aN=q.根据对...