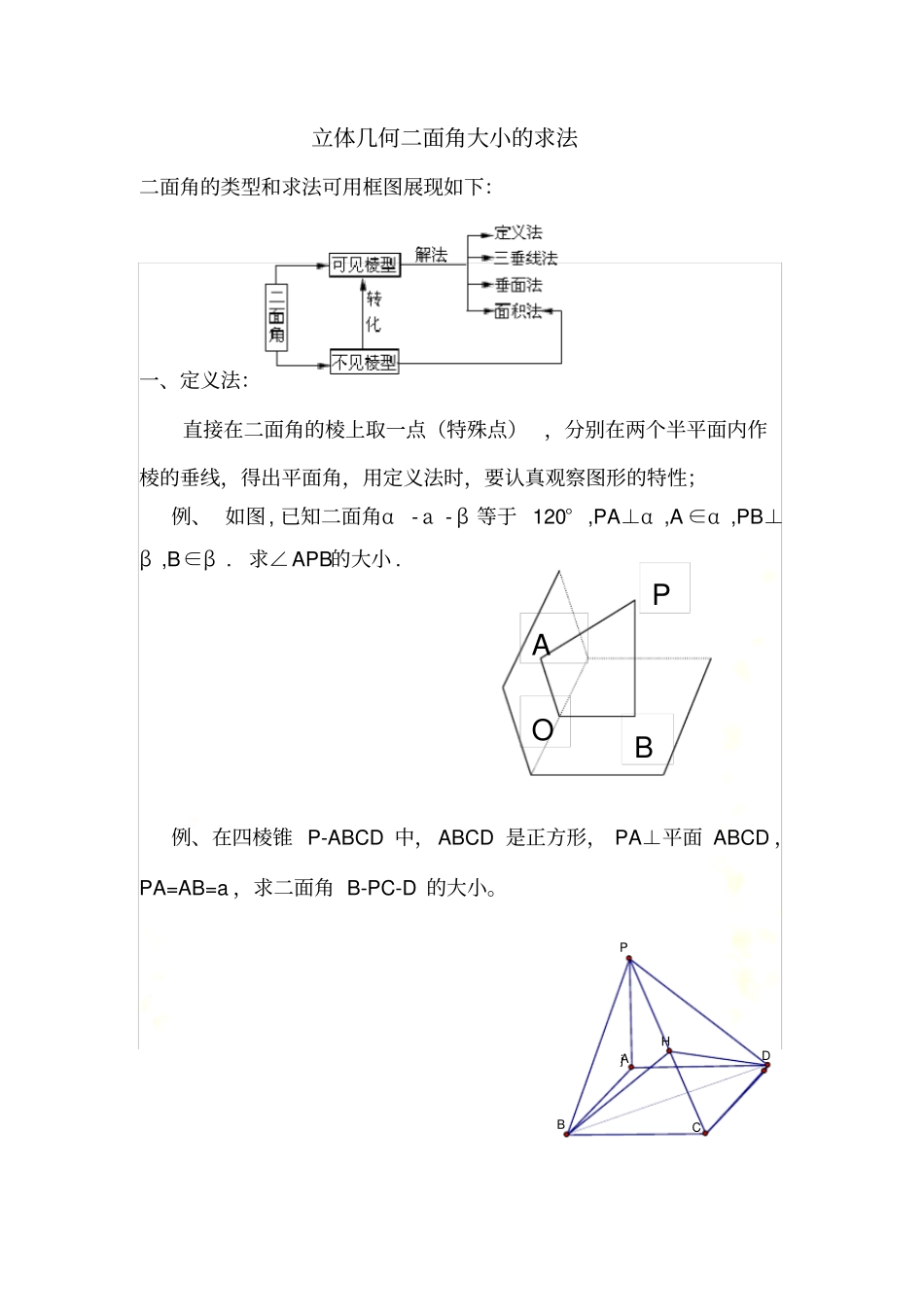
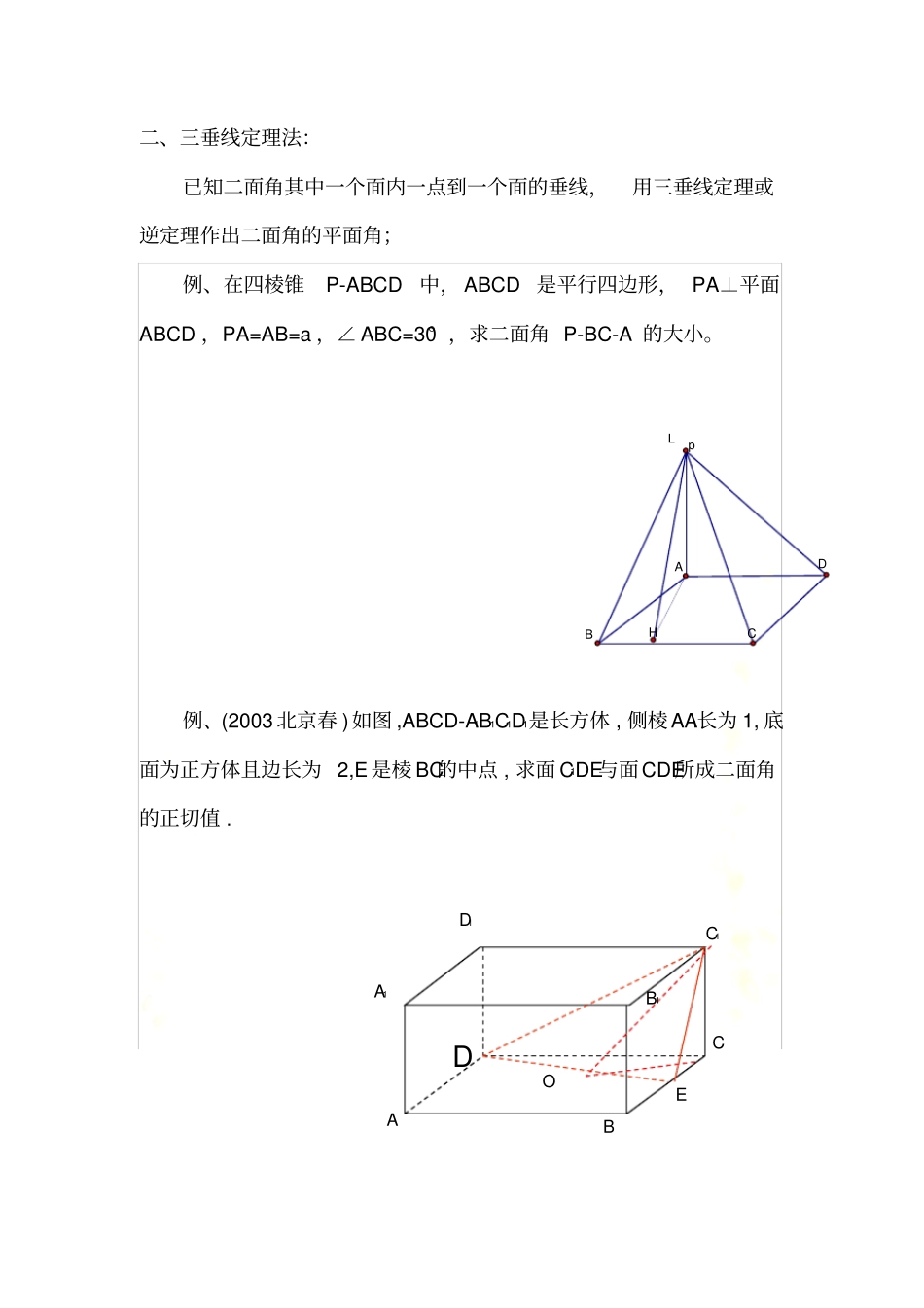
立体几何二面角 5 种常见解法立体几何二面角大小的求法二面角的类型和求法可用框图展现如下:一、定义法:直接在二面角的棱上取一点(特殊点),分别在两个半平面内作棱的垂线,得出平面角,用定义法时,要认真观察图形的特性;例、 如图, 已知二面角α- а - β 等于 120° ,PA⊥α ,A ∈α ,PB⊥β ,B∈β . 求∠APB的大小 . 例、在四棱锥 P-ABCD 中,ABCD 是正方形, PA⊥平面 ABCD ,PA=AB=a ,求二面角 B-PC-D 的大小。jABCDPHP O B A 二、三垂线定理法:已知二面角其中一个面内一点到一个面的垂线,用三垂线定理或逆定理作出二面角的平面角;例、在四棱锥P-ABCD中, ABCD 是平行四边形, PA⊥平面ABCD ,PA=AB=a ,∠ ABC=30° ,求二面角 P-BC-A 的大小。例、(2003 北京春 )如图 ,ABCD-A1B1C1D1是长方体 , 侧棱AA1长为 1, 底面为正方体且边长为 2,E 是棱 BC的中点 , 求面 C1DE与面CDE所成二面角的正切值 . pABCDLHA B C D A1B1C1 D1E O 例、Δ ABC中,∠A=90° ,AB=4,AC=3,平面 ABC外一点 P 在平面 ABC内的射影是 AB中点 M,二面角 P— AC— B的大小为 45° 。求(1)二面角 P— BC— A的大小;(2)二面角 C— PB— A 的大小例、(2006 年陕西试题 )如图 4,平面⊥平面, ∩=l,A∈,B∈,点 A 在直线 l 上的射影为 A 1,点 B 在 l 的射影为 B1,已知AB=2,AA 1=1,BB 1= 2,求:二面角 A 1-AB -B1 的大小 .图 4 B1A A1B L E F C DPMBA三、垂面法:已知二面角内一点到两个面的垂线时,过两垂线作平面与两个半平面的交线所成的角即为平面角,由此可知,二面角的平面角所在的平面与棱垂直;例、空间的点 P到二面角l的面、及棱 l 的距离分别为4、3、3392,求二面角l的大小 . 四、射影法:(面积法)利用面积射影公式S 射=S 原 cos ,其中为平面角的大小,此方法不必在图形中画出平面角;例、在四棱锥 P-ABCD中,ABCD为正方形, PA⊥平面 ABCD,PA=AB=a,求平面 PBA与平面 PDC所成二面角的大小。lABCDPP lC B A 例、如图,设M为正方体 ABCD-A1B1C1D1的棱 CC1的中点,求平面BMD1与底面 ABCD所成的二面角的大小。五、平移或延长(展)线(面)法对于一类没有给出棱的二面角,应先延伸两个半平面, 使之相交出现棱,然后再选用上述方法(尤其要考虑射影法)。例、在四棱锥 P-ABCD 中,ABCD 为正方形,PA⊥平面 ABCD ,PA=AB=a,求平面 PBA 与平面 PDC 所成二面角的大小。A H M D1C1B1A1B C D PC1A1B1ABCDPABCD