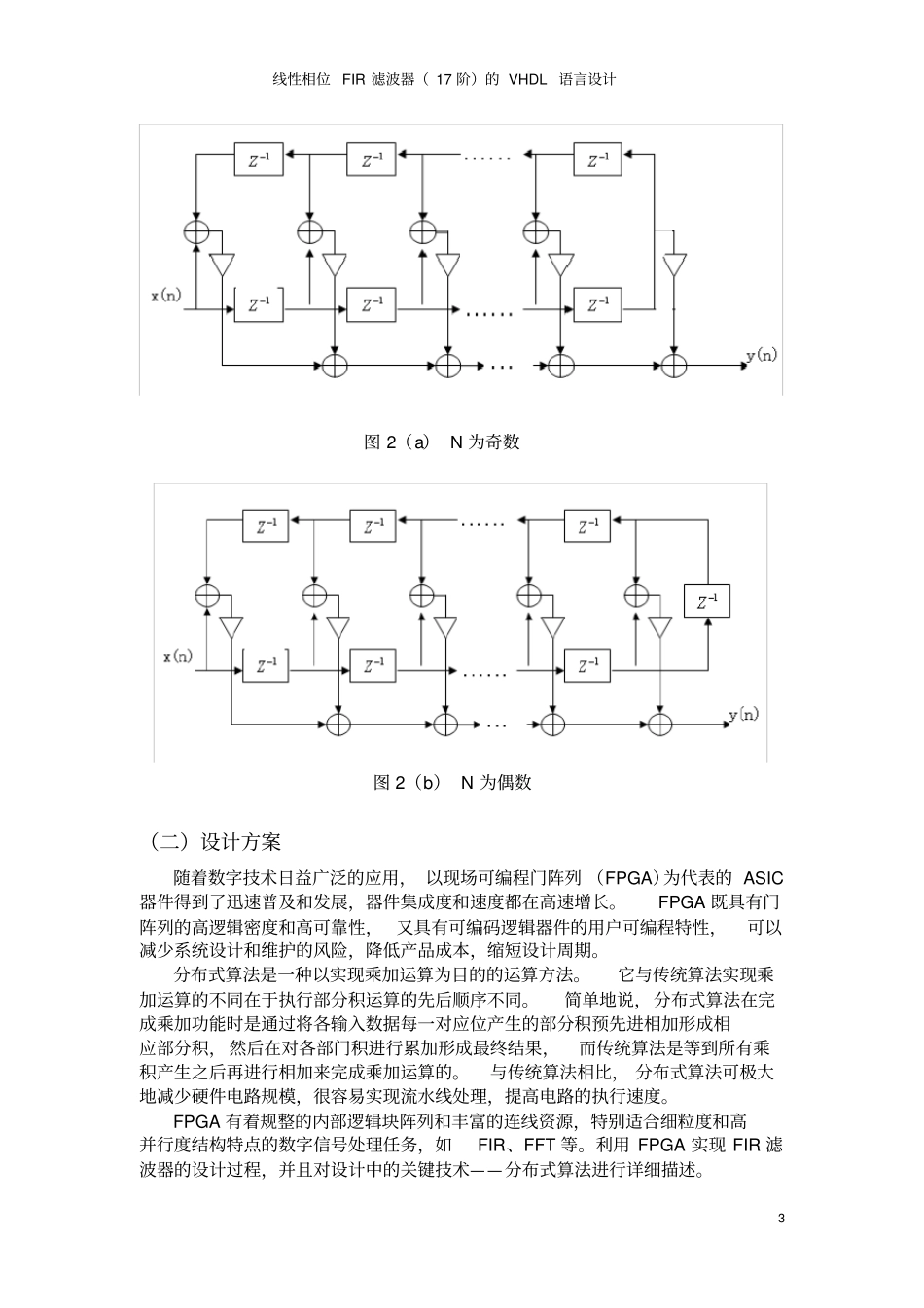
线性相位 FIR 滤波器( 17 阶)的 VHDL 语言设计1 EDA 课程设计报告滤波器设计参数:根据要求,要设计一个输入8 位,输出 8 位的 17 阶线性相位 FIR 滤波器,所以采用图2(a)的方式,其中输入信号范围为:[±99,0,0,0, ±70,0,0,0, ±99,0,0,0, ±70,⋯],此滤波器Fs 为 44kHz,Fc为 10.4kHz。(一) FIR 数字滤波器理论简述有限冲激响应( FIR)数字滤波器和无限冲激响应( IIR )数字滤波器广泛应用于数字信号处理系统中。IIR 数字滤波器方便简单,但它相位的非线性,要求采用全通网络进行相位校正,且稳定性难以保障。FIR 滤波器具有很好的线性相位特性,使得它越来越受到广泛的重视。有限冲击响应( FIR)滤波器的特点:1 既具有严格的线性相位,又具有任意的幅度;2 FIR 滤波器的单位抽样响应是有限长的,因而滤波器性能稳定;3 只要经过一定的延时,任何非因果有限长序列都能变成因果的有限长序列,因而能用因果系统来实现;4 FIR滤波器由于单位冲击响应是有限长的,因而可用快速傅里叶变换(FFT) 算法来实现过滤信号,可大大提高运算效率。5 FIR 也有利于对数字信号的处理,便于编程,用于计算的时延也小,这对实时的信号处理很重要。6 FIR 滤波器比较大的缺点就是阶次相对于IIR 滤波器来说要大很多。FIR 数字滤波器是一个线性时不变系统(LTI ),N阶因果有限冲激响应滤波器可以用传输函数H(z)来描述,0( )( )NkkH zh k z(0.1) 在时域中,上述有限冲激响应滤波器的输入输出关系如下:0[ ][ ][ ][ ] []Nky nx nh nx k h nk(0.2) 其中, x[ n] 和 y[ n] 分别是输入和输出序列。N阶有限冲激响应滤波器要用N+1 个系数描述, 通常要用 N+1个乘法器和 N个两输入加法器来实现。 乘法器的系数正好是传递函数的系数,因此这种结构称为直接型结构,可通过式(1.2 )来实现,如图 1。线性相位 FIR 滤波器( 17 阶)的 VHDL 语言设计2 图 1 当冲击响应满足下列条件时, FIR 滤波器具有对称结构,为线性相位滤波器:。(1.3)这种对称性,可使得乘法器数量减半:对n 价滤波器,当 n 为偶数时,乘法器的个数为 n/2 个;当 n 为奇数时,乘法器的个数为(n+1)/2个。在电路实现中,乘法器占用的逻辑单元数较多。 乘法器的增加, 意味着电路成本增加, 另外对电路的工作速度也有影响。N阶线性相位的因果 FIR 系统的单位冲激响应滤波器可用对称冲...