数字信号处理

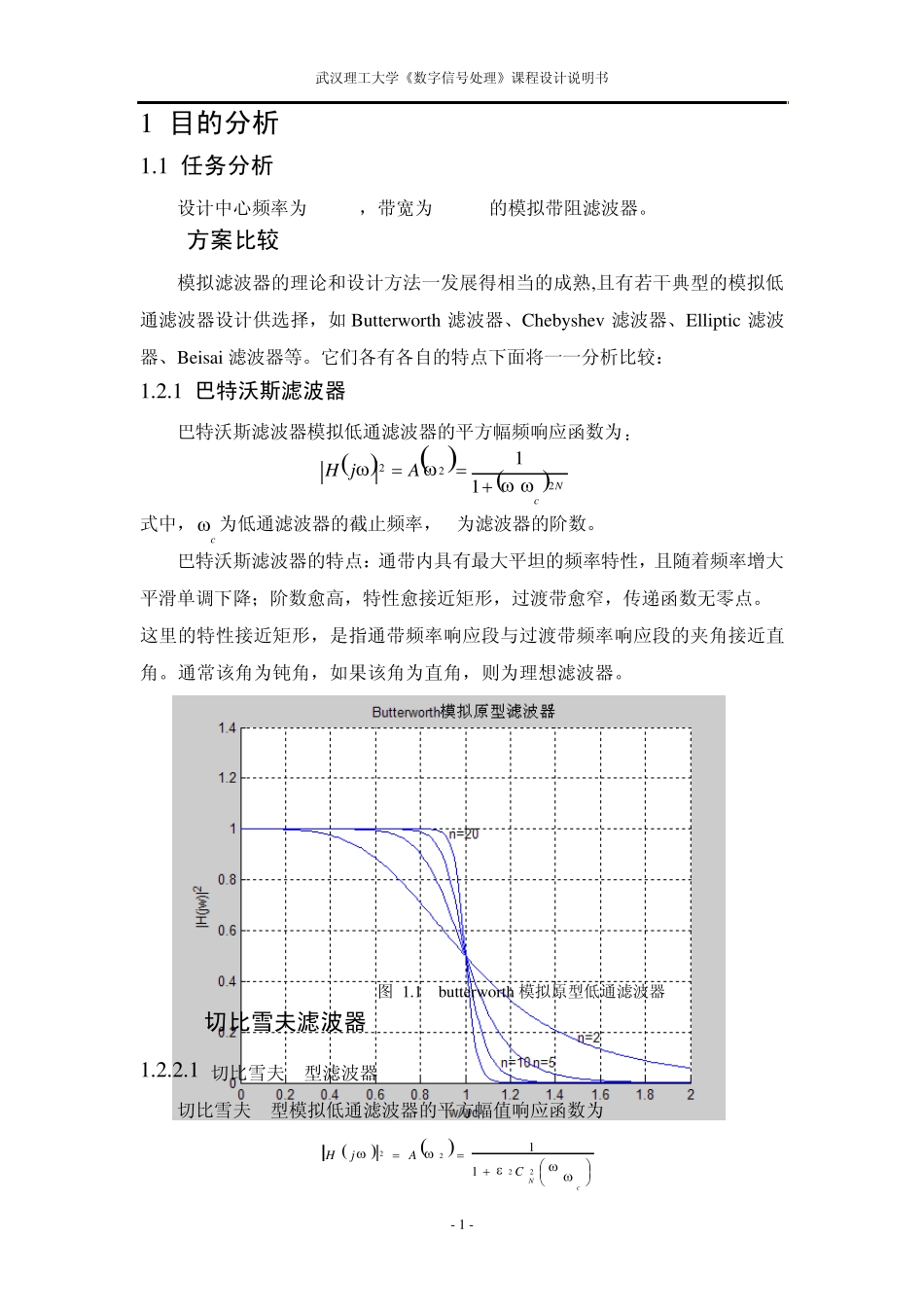
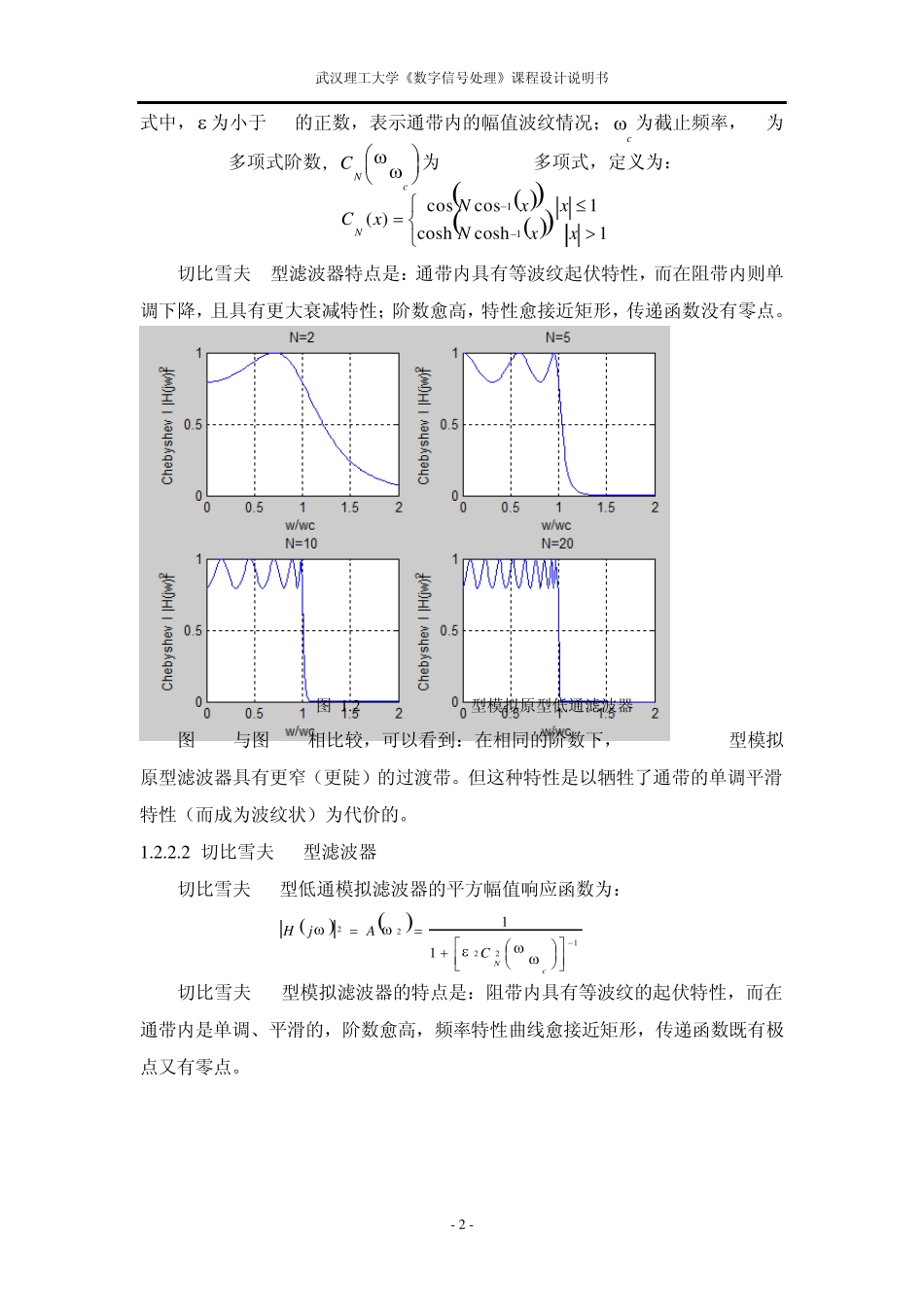
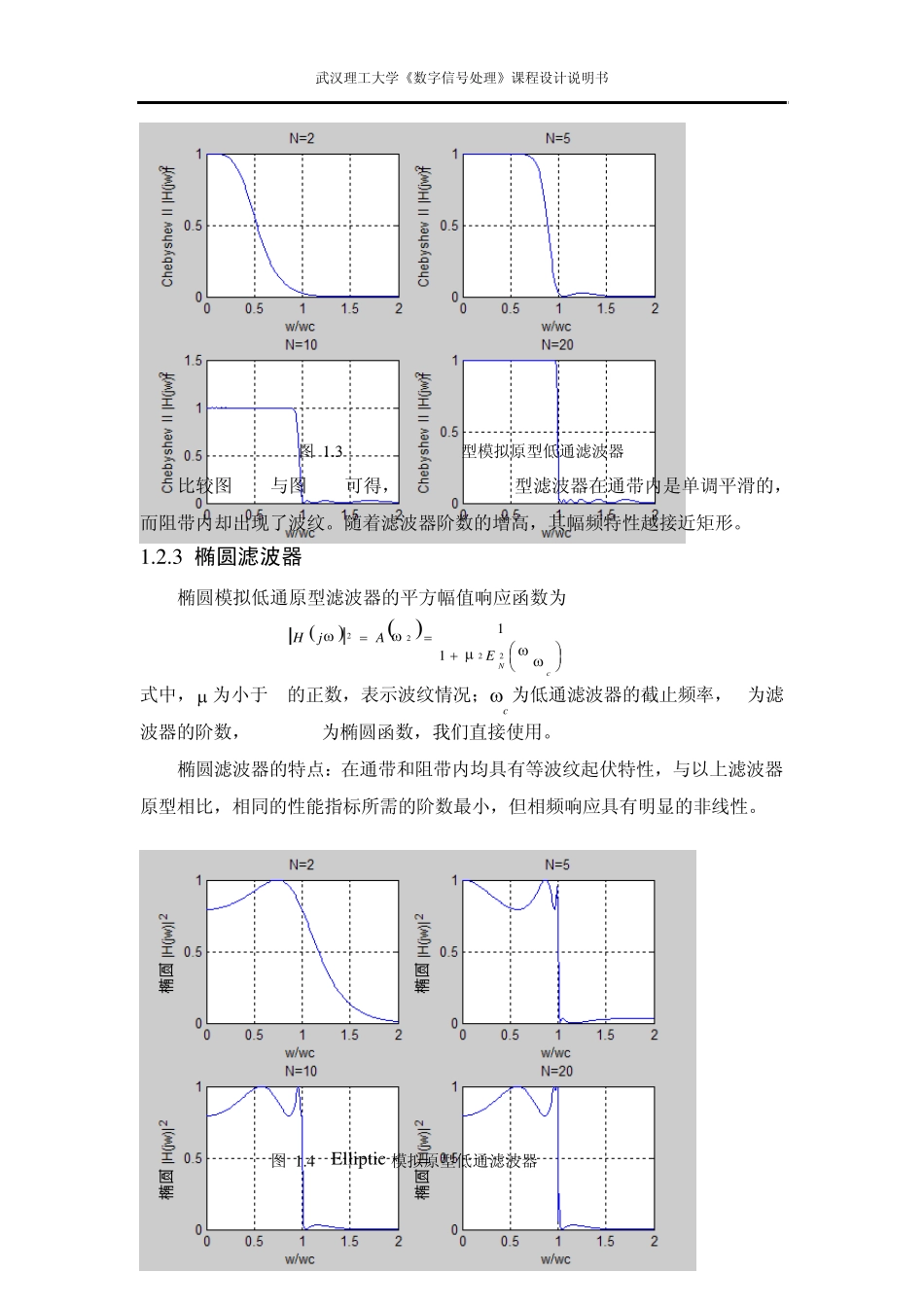
武汉理工大学《数字信号处理》课程设计说明书 - 1 - 1 目的分析 1.1 任务分析 设计中心频率为200Hz，带宽为150Hz的模拟带阻滤波器。 1.2 方案比较 模拟滤波器的理论和设计方法一发展得相当的成熟,且有若干典型的模拟低通滤波器设计供选择，如Butterworth 滤波器、Chebyshev 滤波器、Elliptic 滤波器、Beisai 滤波器等。它们各有各自的特点下面将一一分析比较： 1.2.1 巴特沃斯滤波器 巴特沃斯滤波器模拟低通滤波器的平方幅频响应函数为：   NcAjH22211 (1.1) 式中，c 为低通滤波器的截止频率，N为滤波器的阶数。 巴特沃斯滤波器的特点：通带内具有最大平坦的频率特性，且随着频率增大平滑单调下降；阶数愈高，特性愈接近矩形，过渡带愈窄，传递函数无零点。 这里的特性接近矩形，是指通带频率响应段与过渡带频率响应段的夹角接近直角。通常该角为钝角，如果该角为直角，则为理想滤波器。 图 1.1 butterworth 模拟原型低通滤波器 1.2.2切比雪夫滤波器 1.2.2.1 切比雪夫 I型滤波器 切比雪夫 I型模拟低通滤波器的平方幅值响应函数为 cNCAjH222211 (1.2) 武汉理工大学《数字信号处理》课程设计说明书 - 2 - 式中， 为小于1的正数，表示通带内的幅值波纹情况；c 为截止频率，N为Chebyshev多项式阶数，cNC为Chebyshev多项式，定义为：   1coshcosh1coscos)(11xxNxxNxCN (1.3) 切比雪夫I型滤波器特点是：通带内具有等波纹起伏特性，而在阻带内则单调下降，且具有更大衰减特性；阶数愈高，特性愈接近矩形，传递函数没有零点。 图 1.2 Chebvshev I型模拟原型低通滤波器 图1.1与图1.2相比较，可以看到：在相同的阶数下，Chebyshev I型模拟原型滤波器具有更窄（更陡）的过渡带。但这种特性是以牺牲了通带的单调平滑特性（而成为波纹状）为代价的。 1.2.2.2 切比雪夫II型滤波器 切比雪夫II型低通模拟滤波器的平方幅值响应函数为： 1222211cNCAjH (1.4) 切比雪夫II型模拟滤波器的特点是：阻带内具有等波纹的起伏特性，而在通带内是单调、平滑的，阶数愈高，频率特性曲线愈接近矩形，传递函数既有极点又有零点。 武汉理工大学《数字信号处理》课程设计说明书 - 3 - 图 1.3 Chebvshev II型模拟原型低通滤波器 ...