数字信号处理参考试题3

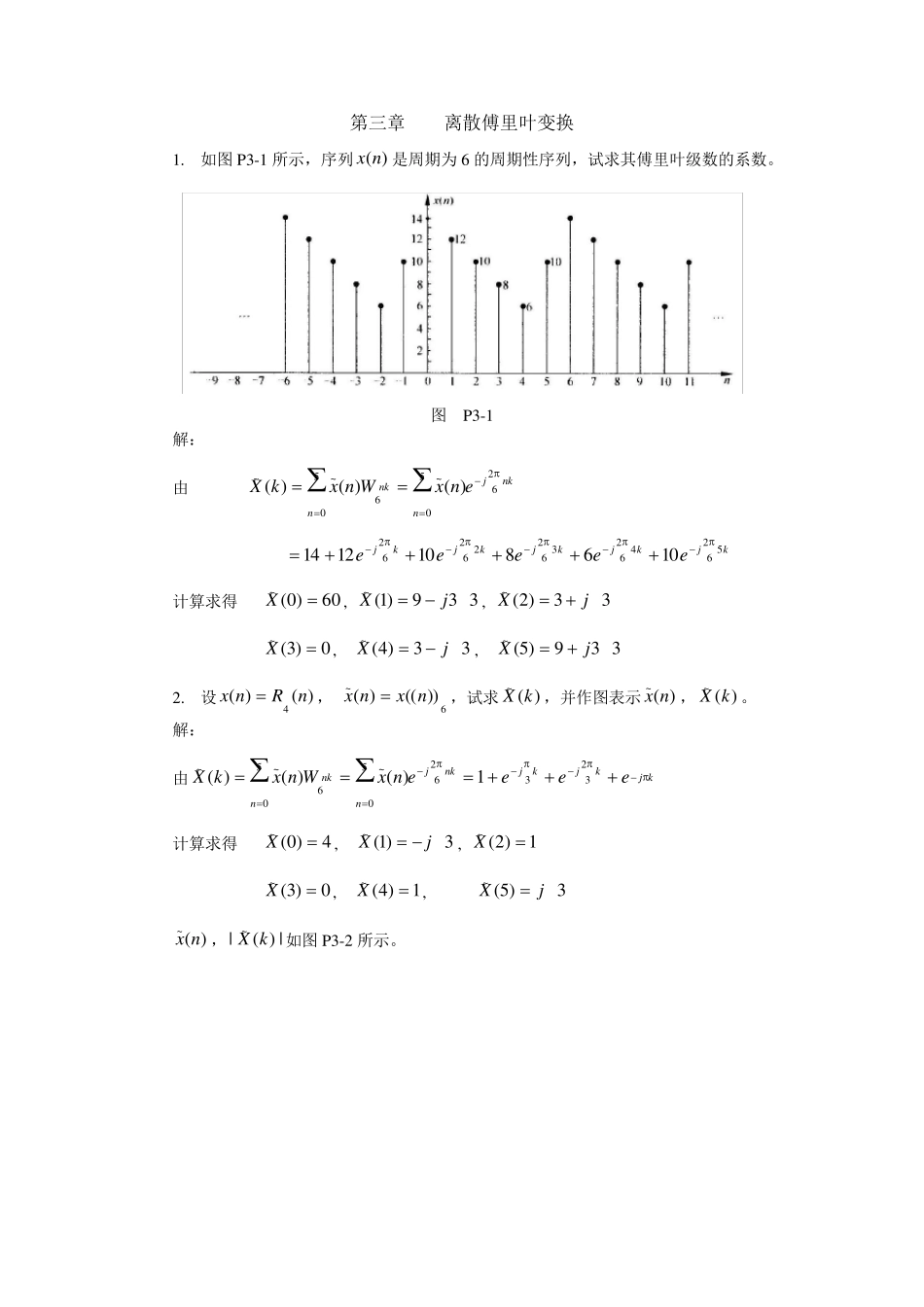
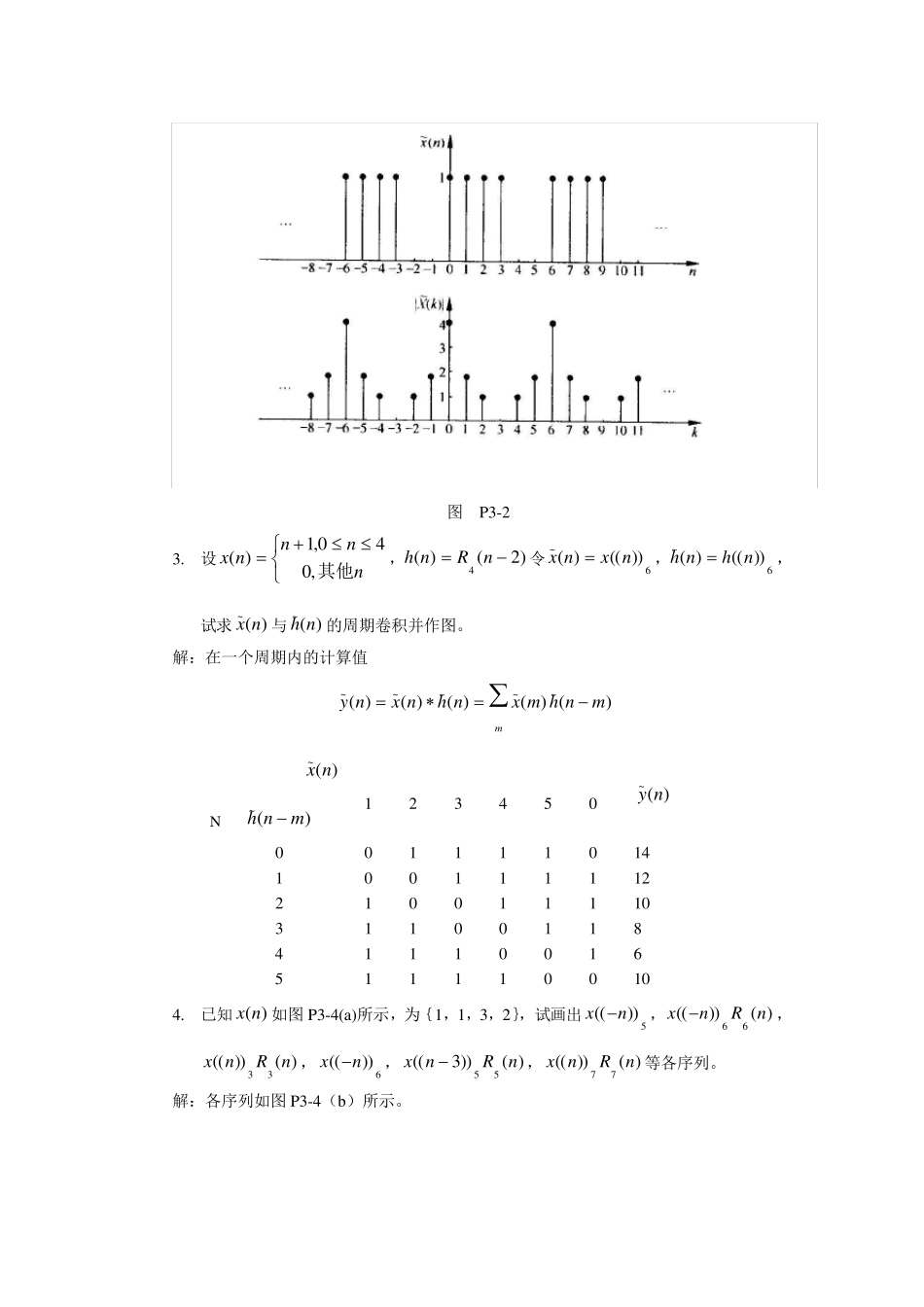
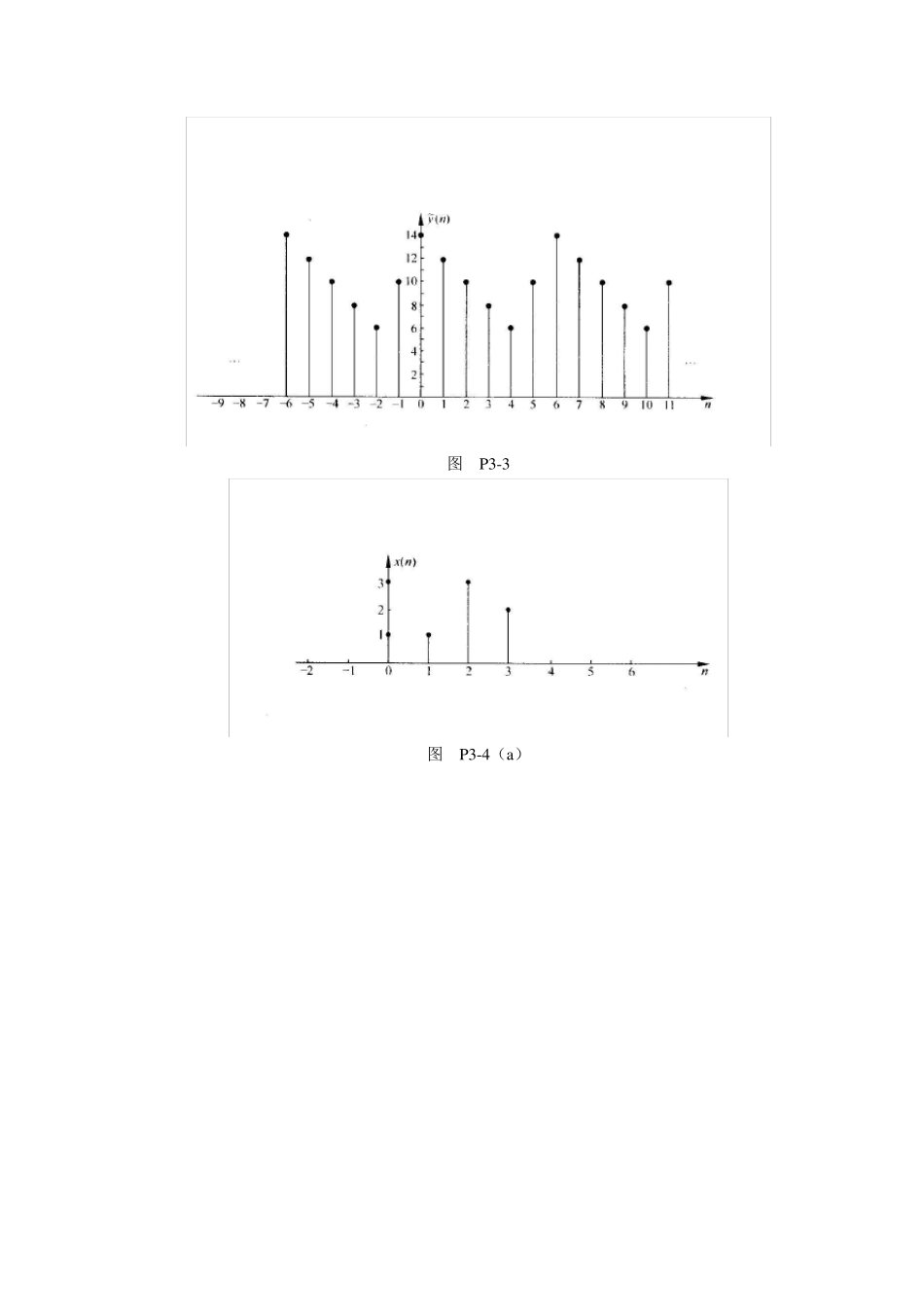
第三章 离散傅里叶变换 1. 如图P3-1 所示，序列)(nx是周期为6 的周期性序列，试求其傅里叶级数的系数。 图 P3-1 解： 由 nkjnnnkenxWnxkX6250~506~~)()()( kjkjkjkjkjeeeee562462362262621068101214 计算求得 60)0(~X, 339)1(~jX, 33)2(~jX 0)3(~X, 33)4(~jX, 339)5(~jX 2. 设)()(4 nRnx， 6~))(()(nxnx，试求)(~kX，并作图表示)(~ nx，)(~kX。 解： 由kjkjkjnkjnnnkeeeenxWnxkX3236250~506~~1)()()( 计算求得 4)0(~X, 3)1(~jX, 1)2(~X 0)3(~X, 1)4(~X, 3)5(~jX )(~ nx， |)(|~kX如图P3-2 所示。 图 P3-2 3. 设nnnnx其他,040,1)(，)2()(4nRnh令6~))(()(nxnx，6~))(()(nhnh，试求)(~ nx与)(~ nh的周期卷积并作图。 解：在一个周期内的计算值 mmnhmxnhnxny)()()()()(~~~~~ )(~ nx N )(~mnh 1 2 3 4 5 0 )(~ ny 0 0 1 1 1 1 0 14 1 0 0 1 1 1 1 12 2 1 0 0 1 1 1 10 3 1 1 0 0 1 1 8 4 1 1 1 0 0 1 6 5 1 1 1 1 0 0 10 4. 已知)(nx如图P3-4(a)所示，为｛1，1，3，2｝，试画出5))(( nx ，)())((66nRnx ，)())((33nRnx，6))(( nx ，)())3((55nRnx，)())((77nRnx等各序列。 解：各序列如图P3-4（b）所示。 图 P3-3 图 P3-4（a） 图 P3-4（b） 5. 试求以下有限长序列的 N 点 DFT（闭合形式表达式）： (1))()cos()(0nRnanxN (2) )()(nRanxNn (3) Nnnnnx00 0),()( (4) )()(nnRnxN (5) )()(2nRnnxN 解： （1）因为)()cos()(0nRnanxN，所以 )()(21)()cos()(102102000kReeeakRenakXNNnnkNjnjnjNnNnkNj )(2110210200kReeaNNnnkNjNnnkNj )(111121000022kReeeeaNkNjNjkNjNj )()()()(21000000000000221221221222221221221222...