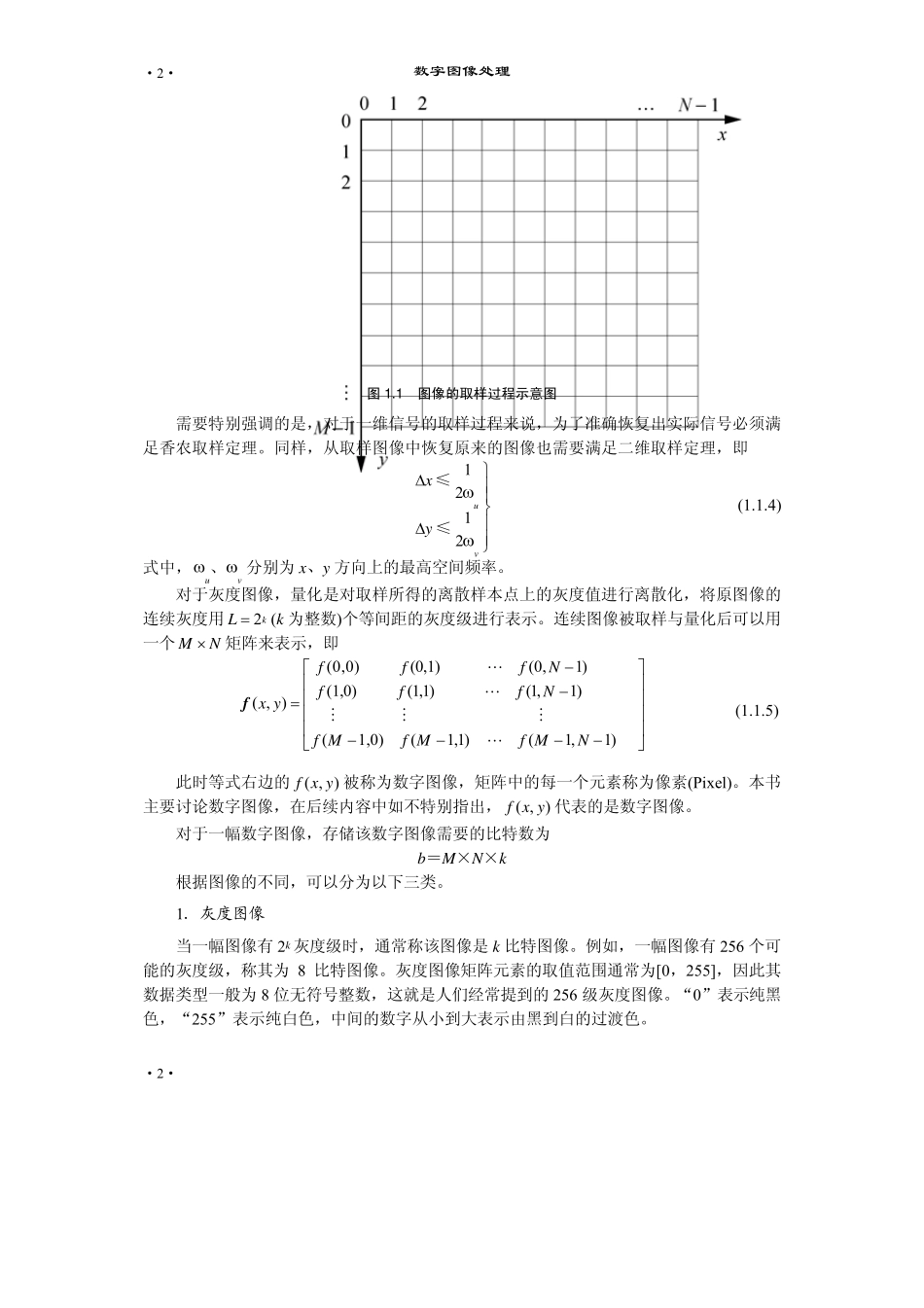
第1 章 数字图像处理的基本知识 1 .1 数字图像和图像处理 1 .1 .1 图像的概念 图像是与之对应的景物的一个表示,一幅空间三维的、动态的图像可以定义为 ( , , , )If x y z t= (1.1.1) 式中,x,y,z 是空间变量;t 是时间变量。在实际应用中,图像可以借助不同的方式来获得。目前普遍采用的一种方式是利用一定电磁能量谱波段内的电磁波来成像,可从可见光扩展到其他频段,在低频端,有红外线、微波等;在高频端,有紫外光、X 光、γ 射线、宇宙射线等。如红外成像是利用物体自然发射的红外辐射或运用不同物体对红外辐射的不同反射率进行成像。此时图像可以用式(1.1.2)表示为 ( , , , , )If x y ztλ= (1.1.2) 式中,λ 是波长。 λ 不同,物体的反射、发射或吸收特性不同,所得到的图像也不同。一幅图像记录的是物体辐射能量的空间分布,一般是灰度图,这时 f 为辐射度对应的灰度值。当对可见光成像时,灰度值对应客观景物被观察到的亮度。 除了用电磁波成像方式以外,成像还可以借助于其他方式来实现,如声波、超声波、电子束、磁共振等,本书将在后续内容中介绍它们的成像原理。 一般情况下只考虑平面、单色、静止图像,此时图像可表示为一个二维函数: ( , )If x y= (1.1.3) 1 .1 .2 数字图像及其表示 传统意义上的图像是连续的,即式(1.1.3)中的x、y、f 是连续的,表示的是物体辐射能量在空间上的连续分布,连续图像也称为模拟图像。 为了便于利用计算机对图像进行进一步的加工和处理,需要把模拟图像在空间上、幅值上进行离散化,将其转换为对应的数字形式,离散化了的图像称为数字图像。图像的离散化过程包括两种处理:取样和量化。一幅模拟图像的坐标及幅度都是连续的,为了把它转换为数字形式,必须对坐标和幅度都作离散化操作。数字化坐标值称为取样,它确定了图像的空间分辨率;数字化幅度值称为量化,它确定了图像的幅度分辨率。 以均匀取样为例,模拟图像的取样过程可以用图1.1 示意(本书以图像左上方的顶点为原点,向右延伸的方向为 x 轴,向下延伸的方向为 y 轴)。假设沿空间x 轴方向的取样间隔为等间距 x∆ ,沿 y 轴方向的取样间隔为等间距 y∆ ,则均匀取样过程可看作将图像平面划分为规则、均匀的网格,每个网格的位置由 x,y 表示,x 的取值范围为[0, M-1],M 为沿 x方向的取样点数;y 的取值范围为[0, N-1],N 为沿 y 方向的取样点数。 数...