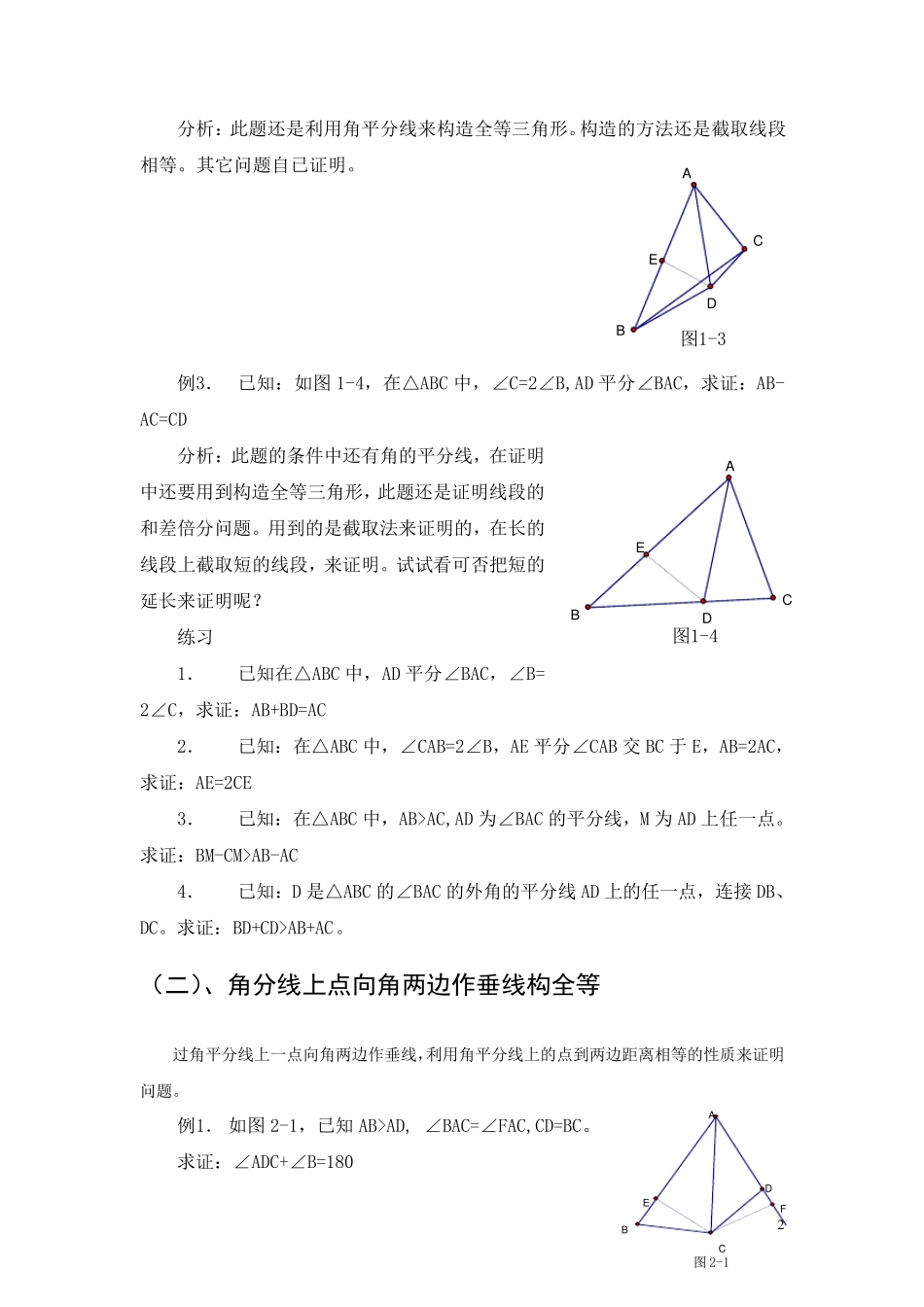
1 由角平分线想到的辅助线 角平分线具有两条性质:a、对称性;b、角平分线上的点到角两边的距离相等。对于有角平分线的辅助线的作法,一般有两种。 ①从角平分线上一点向两边作垂线; ②利用角平分线,构造对称图形(如作法是在一侧的长边上截取短边)。 通常情况下,出现了直角或是垂直等条件时,一般考虑作垂线;其它情况下考虑构造对称图形。至于选取哪种方法,要结合题目图形和已知条件。 与角有关的辅助线 (一)、截取构全等 如图1-1,∠AOC=∠BOC,如取OE=OF,并连接 DE、DF,则有△OED≌△OFD,从而为我们证明线段、角相等创造了条件。 例1. 如图1-2,AB//CD,BE 平分∠ABC,CE 平分∠BCD,点E 在AD 上,求证:BC=AB+CD。 分析:此题中就涉及到角平分线,可以利用角平分线来构造全等三角形,即利用解平分线来构造轴对称图形,同时此题也是证明线段的和差倍分问题,在证明线段的和差倍分问题中常用到的方法是延长法或截取法来证明,延长短的线段或在长的线段长截取一部分使之等于短的线段。但无论延长还是截取都要证明线段的相等,延长要证明延长后的线段与某条线段相等,截取要证明截取后剩下的线段与某条线段相等,进而达到所证明的目的。 简证:在此题中可在长线段 BC 上截取BF=AB,再证明 CF=CD,从而达到证明的目的。这里面用到了角平分线来构造全等三角形。另外一个全等自已证明。此题的证明也可以延长BE 与CD 的延长线交于一点来证明。自已试一试。 例2. 已知:如图1-3,AB=2AC,∠BAD=∠CAD,DA=DB,求证 DC⊥AC 图1-1OABDEFC图1-2ADBCEF 2 分析:此题还是利用角平分线来构造全等三角形。构造的方法还是截取线段相等。其它问题自已证明。 例3. 已知:如图1-4,在△ABC 中,∠C=2∠B,AD 平分∠BAC,求证:AB-AC=CD 分析:此题的条件中还有角的平分线,在证明中还要用到构造全等三角形,此题还是证明线段的和差倍分问题。用到的是截取法来证明的,在长的线段上截取短的线段,来证明。试试看可否把短的延长来证明呢? 练习 1. 已知在△ABC 中,AD 平分∠BAC,∠B=2∠C,求证:AB+BD=AC 2. 已知:在△ABC 中,∠CAB=2∠B,AE 平分∠CAB 交 BC 于 E,AB=2AC,求证:AE=2CE 3. 已知:在△ABC 中,AB>AC,AD 为∠BAC 的平分线,M 为 AD 上任一点。求证:BM-CM>AB-AC 4. 已知:D 是△ABC 的∠BAC 的外角的平分线AD 上的任一点,连接 DB、DC。求证:BD+CD>AB+AC。 (二...