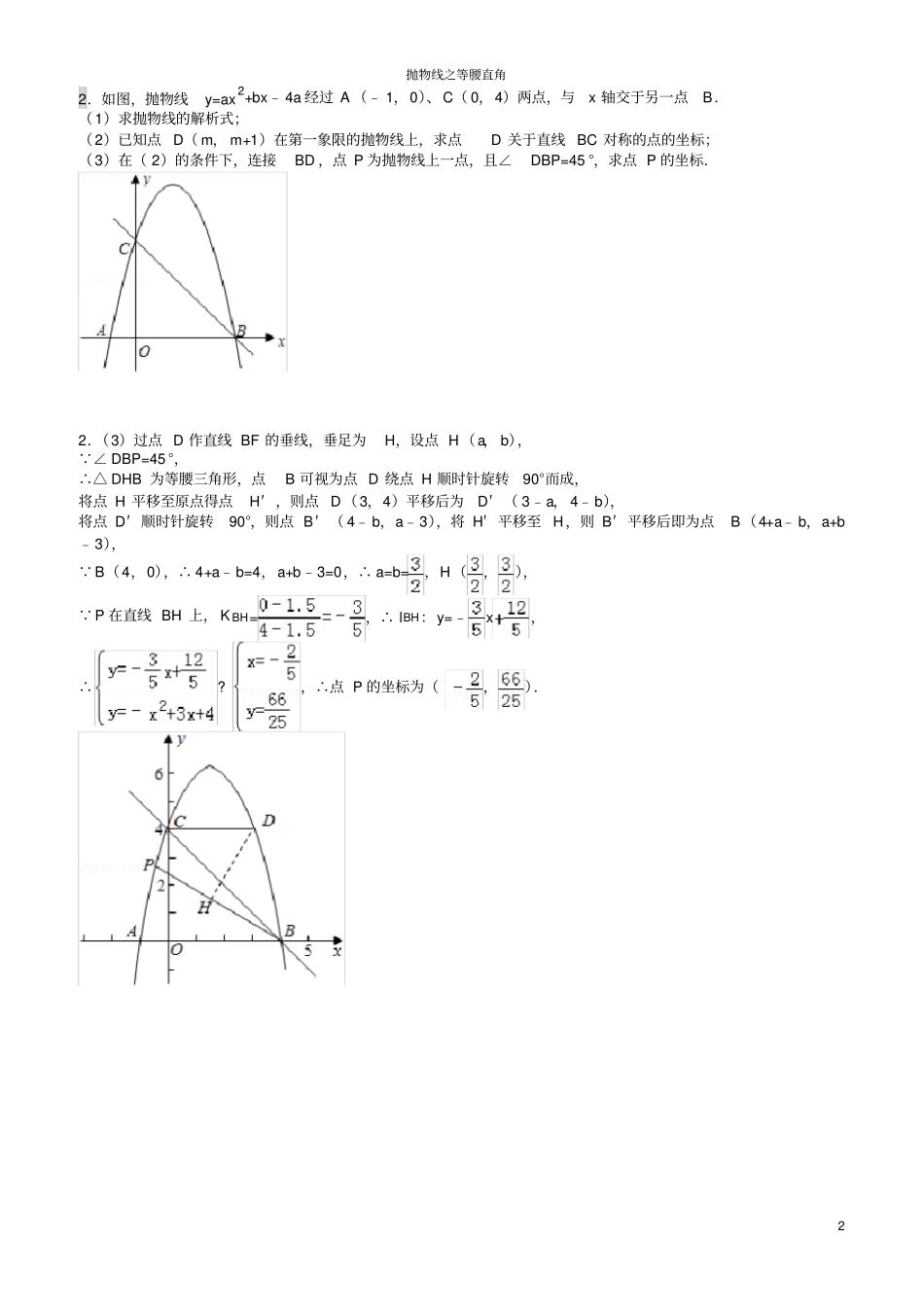
抛物线之等腰直角1 1.如图, 抛物线 y=﹣x2+bx+c 与直线 y=x+2 交于 C、D 两点, 其中点 C 在 y 轴上, 点 D 的坐标为 (3,).(1)求抛物线的解析式;(2)点 P 是 y 轴右侧的抛物线上一个动点,过点P 作 PE⊥ x 轴于点 E,交直线 CD 于点 F.若点 P 的横坐标为 m,设线段 PF 的长度为 y,求 y 与 m 之间的函数关系式,并直接写出自变量m 的取值范围;(3)在( 2)的条件下,是否存在点P,使∠ PCF=45°?若存在,求出点P 的坐标;若不存在,请说明理由.(3)过 P 点作 CD 的垂线,垂足为N, ∠ PCF=45°,∴△ PCN 为等腰直角三角形,点P 可视为点 C 绕点 N 顺时针旋转90°而成, N 点在直线 CD 上,∴设 N(t,t+2),C( 0,2),将 N 点平移至原点,N(0,0),则 C′ (﹣ t,﹣t),将 C′ 点绕原点顺时针旋转90°,则 P′ (﹣t,t),将 N′ 点平移至N 点,则 P 平移后即为P(t,t+2),把 P 点代入抛物线,∴,∴ t1=0(舍),t2=1,∴符合条件的点P 的坐标为(,)或(,).抛物线之等腰直角2 2.如图,抛物线y=ax2+bx﹣ 4a 经过 A (﹣ 1,0)、C( 0,4)两点,与x 轴交于另一点B.(1)求抛物线的解析式;(2)已知点 D( m, m+1)在第一象限的抛物线上,求点D 关于直线 BC 对称的点的坐标;(3)在( 2)的条件下,连接BD ,点 P 为抛物线上一点,且∠DBP=45 °,求点 P 的坐标.2.(3)过点 D 作直线 BF 的垂线,垂足为H,设点 H(a, b), ∠ DBP=45 °,∴△ DHB 为等腰三角形,点B 可视为点 D 绕点 H 顺时针旋转90°而成,将点 H 平移至原点得点H′ ,则点 D(3,4)平移后为D′ ( 3﹣a, 4﹣b),将点 D′ 顺时针旋转90°,则点 B′ ( 4﹣ b,a﹣3),将 H′ 平移至 H,则 B′ 平移后即为点B(4+a﹣ b,a+b﹣3), B(4,0),∴ 4+a﹣b=4,a+b﹣3=0,∴ a=b=,H(,), P 在直线 BH 上, K BH=,∴ lBH:y=﹣x,∴?,∴点 P 的坐标为(,).抛物线之等腰直角3 3.如图, 抛物线 y=x2+bx+c 与直线 y=x﹣ 3 交于 A 、B 两点, 其中点 A 在 y 轴上, 点 B 坐标为(﹣ 4,﹣5),点 P 为 y 轴左侧的抛物线上一动点,过点P 作 PC⊥x 轴于点 C,交 AB 于点 D.(1)求抛物线的解析式;(2)以 O,A ,P,D 为顶点的平行四边...