9.5利用柱面坐标和球面坐标计算三重积分

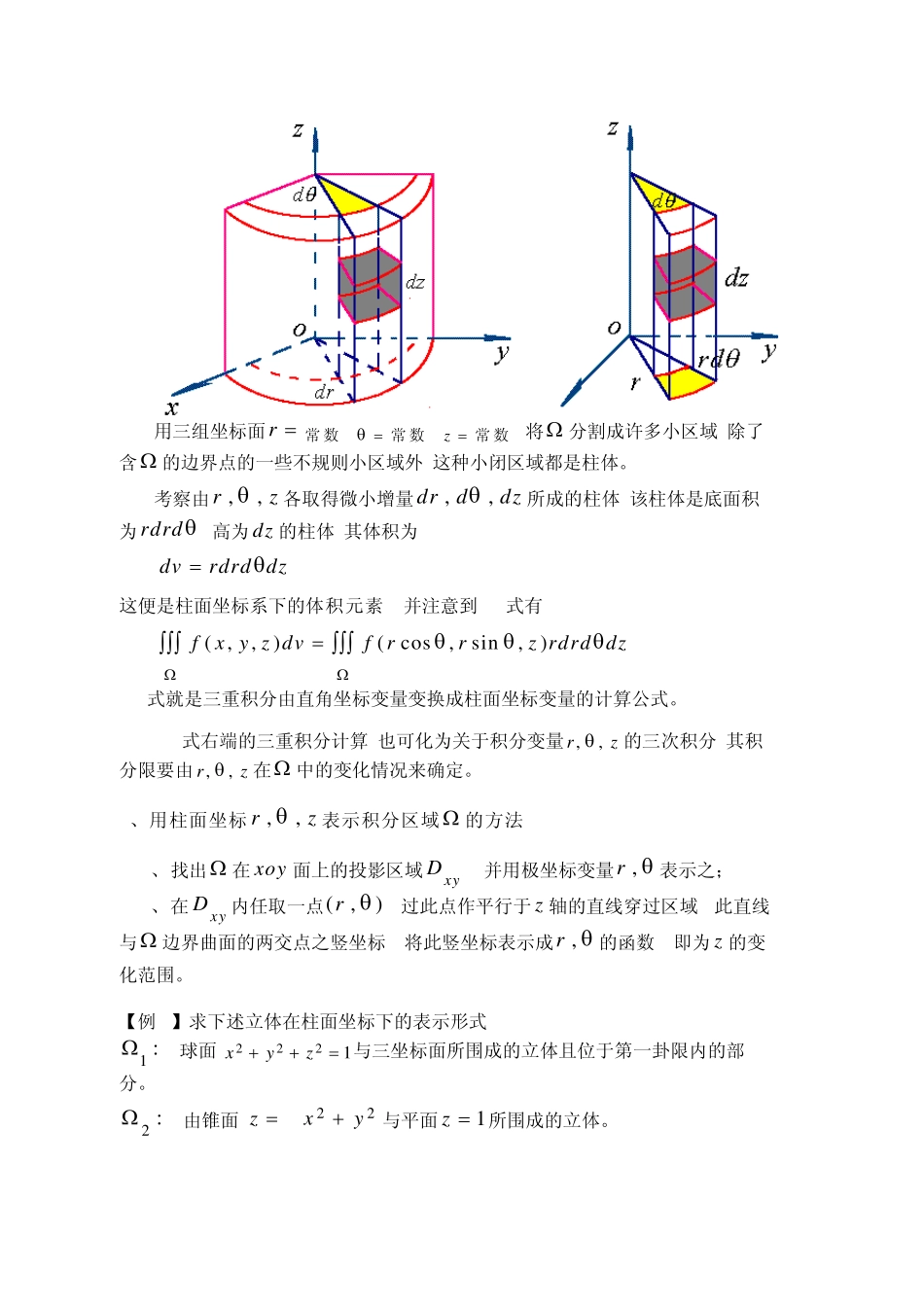
§9.5 利用柱面坐标和球面坐标计算三重积分 对于某些三重积分,由于积分区域和被积函数的特点,往往要利用柱面坐标和球面坐标来计算。 一、利用柱面坐标计算三重积分 1、柱面坐标 设 Mx y z( ,,) 为空间的一点,该点在 xoy 面上的投影为 P ,P 点的极坐标为r ,  ,则rz,,三个数称作点 M 的柱面坐标。 规定rz,,的取值范围是 0  r，02 ，  z 柱面坐标系的三组坐标面分别为 r  常 数 ,即以 z 轴为轴的圆柱面；   常 数 ,即过 z 轴的半平面； z  常 数 ,即与 xoy 面平行的平面。 点 M 的直角坐标与柱面坐标之间有关系式 xryrzzcossin (1) 2、三重积分fx y z dv( ,,)在柱面坐标系中的计算公式 用三组坐标面r  常数,  常数,z  常数,将 分割成许多小区域,除了含 的边界点的一些不规则小区域外,这种小闭区域都是柱体。 考察由rz,,各取得微小增量drddz,,所成的柱体,该柱体是底面积为rdrd ,高为dz 的柱体,其体积为 dvrdrd dz 这便是柱面坐标系下的体积元素, 并注意到(1)式有 fx y z dvf rrz rdrd dz( ,,)(cos ,sin,) (2) (2)式就是三重积分由直角坐标变量变换成柱面坐标变量的计算公式。 (2)式右端的三重积分计算,也可化为关于积分变量zr,, 的三次积分,其积分限要由zr,, 在 中的变化情况来确定。 3、用柱面坐标rz,,表示积分区域 的方法 (1)、找出 在xoy 面上的投影区域D xy , 并用极坐标变量r ,  表示之； (2)、在D xy 内任取一点(,)r  , 过此点作平行于z 轴的直线穿过区域, 此直线与 边界曲面的两交点之竖坐标( 将此竖坐标表示成r ,  的函数 )即为z 的变化范围。 【例 1】求下述立体在柱面坐标下的表示形式 1 : 球面xyz2221 与三坐标面所围成的立体且位于第一卦限内的部分。  2 : 由锥面zxy22 与平面z  1所围成的立体。 1 在xoy 面上的投影区域为 Dxyxyxy( ) :,,122100, 其极坐标下的表示形式为 0201,r z 在1 的变化范围是 0122zxy, 即 012zr 故 120201 01:,,rzr  2 在xoy 面上的投影区域为 Dxyxy() :2221, 其极坐标下的表示形式为 0201 ,r z 在...