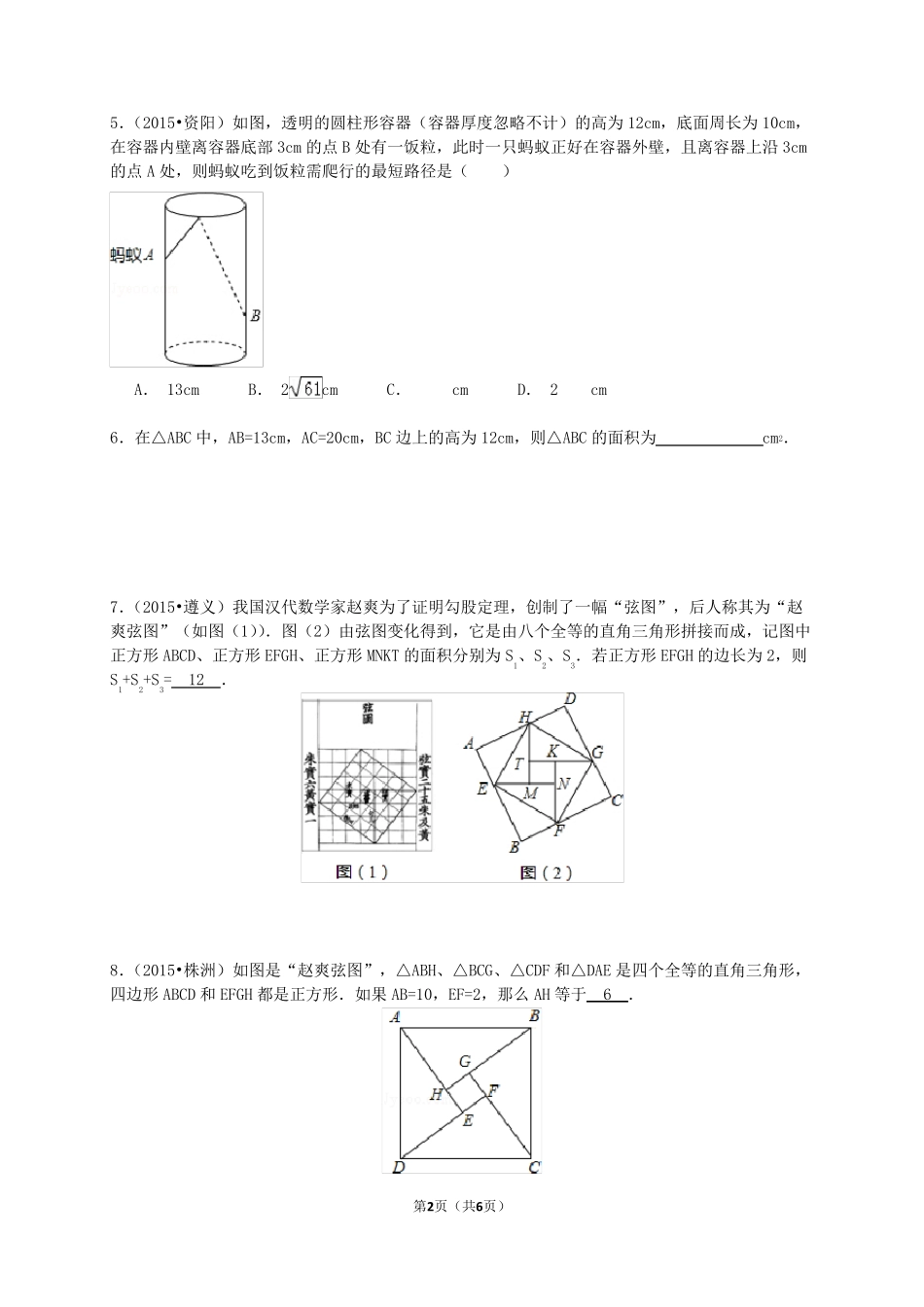
第1页(共6页) 勾股定理和一次函数 1.(2015•大连)如图,在△ABC 中,∠C=90°,AC=2,点D 在BC 上,∠ADC=2∠B,AD=,则BC的长为( ) A. ﹣1 B. +1 C. ﹣1 D. +1 2.(2015•黑龙江)△ABC 中,AB=AC=5,BC=8,点P 是BC 边上的动点,过点P 作PD⊥AB 于点D,PE⊥AC 于点E,则PD+PE 的长是( ) A. 4.8 B. 4.8 或3.8 C. 3.8 D. 5 3.(2015•天水)如图,在四边形ABCD 中,∠BAD=∠ADC=90°,AB=AD=2,CD=,点P 在四边形ABCD 的边上.若点P 到BD 的距离为,则点P 的个数为( ) A. 2 B. 3 C. 4 D. 5 4.(2015•烟台)如图,正方形ABCD 的边长为2,其面积标记为S1,以CD 为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,…按照此规律继续下去,则S2015的值为( ) A. ()2012 B. ()2013 C. ()2012 D. ()2013 第2页(共6页) 5.(2015•资阳)如图,透明的圆柱形容器(容器厚度忽略不计)的高为12cm,底面周长为10cm,在容器内壁离容器底部3cm 的点B 处有一饭粒,此时一只蚂蚁正好在容器外壁,且离容器上沿3cm的点A 处,则蚂蚁吃到饭粒需爬行的最短路径是( ) A. 13cm B. 2cm C. cm D. 2cm 6.在△ABC 中,AB=13cm,AC=20cm,BC 边上的高为12cm,则△ABC 的面积为 cm2. 7.(2015•遵义)我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”(如图(1)).图(2)由弦图变化得到,它是由八个全等的直角三角形拼接而成,记图中正方形ABCD、正方形EFGH、正方形MNKT 的面积分别为S1、S2、S3.若正方形EFGH 的边长为2,则S1+S2+S3= 12 . 8.(2015•株洲)如图是“赵爽弦图”,△ABH、△BCG、△CDF 和△DAE 是四个全等的直角三角形,四边形ABCD 和 EFGH 都是正方形.如果 AB=10,EF=2,那么 AH 等于 6 . 第3页(共6页) 9.(2015•东营)如图,一只蚂蚁沿着边长为2 的正方体表面从点A 出发,经过3 个面爬到点B,如果它运动的路径是最短的,则AC 的长为 . 10.(2015•庆阳)在底面直径为2cm,高为3cm 的圆柱体侧面上,用一条无弹性的丝带从A 至C 按如图所示的圈数缠绕,则丝带的最短长度为 cm.(结果保留π) 11.(2015•柳州)如图,在△ABC 中,D 为AC 边的中点,且DB⊥BC,BC=4,CD=5. (1)求 DB 的长; ...