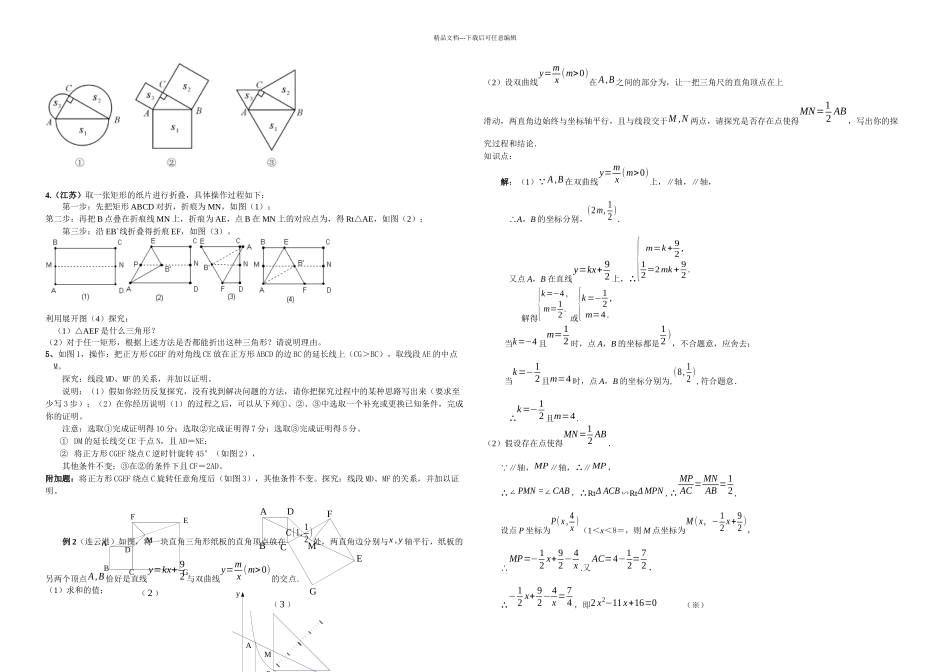
CGIJECBABEKHFBAͼ2ͼ1CABCAB精品文档---下载后可任意编辑探究性问题涉及的基础知识非常广泛,题目没有固定的形式,因此没有固定的解题方法。它既能充分地考查学生的基础知识掌握的熟悉程度,又能较好的考查学生的观察、分析、比较、概括的能力,发散思维能力等,因此复习中既要重视基础知识的复习,又要加强变式训练和数学思想方法的讨论,切实提高分析问题、解决问题的能力。例 1(宜昌课改)如图 1,已知△ABC 的高 AE=5,BC=,∠ABC=45°,F 是 AE 上的点,G 是点 E 关于 F的对称点,过点 G 作 BC 的平行线与 AB 交于 H、与 AC 交于 I,连接 IF 并延长交 BC 于 J,连接 HF 并延长交 BC 于K.(1)请你探究并推断四边形 HIKJ 是怎样的四边形?并对你得到的结论予以证明;(2)当点 F 在 AE 上运动并使点 H、I、K、J 都在△ABC 的三条边上时,求线段 AF 长的取值范围.(图 2 供思考用)解:(1) 点 G 与点 E 关于点 F 对称,GF=FE∴HI BC ∥,∴∠GIF=∠EJF,又 ∠GFI=∠EFJ,GFIEFJ∴△≌△,GI=JE∴同理可得 HG=EK ,HI=JK, ∴∴四边形 HIKJ 是平行四边形(注:说明四边形 HIJK 是平行四边形评 1 分,利用三角形全等说明结论的正确性评 2 分)(2)当 F 是 AE 的中点时,A、G 重合,所以如图 1, AE 过平行四边形 HIJK 的中心 F,HG=EK, GI=JE.HG/BE=GI/EC.∴∴CE >BE,GI∴> HG, CK∴>BJ. ∴当点 F 在 AE 上运动时, 点 K、J 随之在 BC 上运动, 图 1如图 2,当点 F 的位置使得 B、J 重合时,这时点 K 仍为 CE 上的某一点(不与 C、E 重合),而且点 H、I 也分别在 AB、AC 上(这里为独立评分点,以上过程只要叙述大体清楚,说理较为明确即可评 2 分,不说明者不评分,知道要说理但部分不正确者评 1 分)设 EF=x, ∠AHG=∠ABC=45°,AE=5,∴BE=5=GI,AG=HG=5-2x ,CE=403 -5 △AGI∽△AEC,∴AG∶AE=GI∶CE.∴(5-2x)∶5=5∶(403 -5)∴AF=5-x=4∴52 <AF≤4 图 2说明:本题考查知识较多,主要考查了全等三角形、平行四边形、相似形的判定及应用。练习一1、(2024 年盐城)在探讨圆周角与圆心角的大小关系时,小亮首先考虑了一种特别情况(圆心在圆周角的一边上)如图(1)所示: ∠AOC 是⊿ABO 的外角∴∠AOC=∠ABO+∠BAO又 OA=OB∴OAB=OBA ∠∠∴AOC=2ABO∠∠即∠ABC=12AOC∠假如∠ABC 的两边都不...