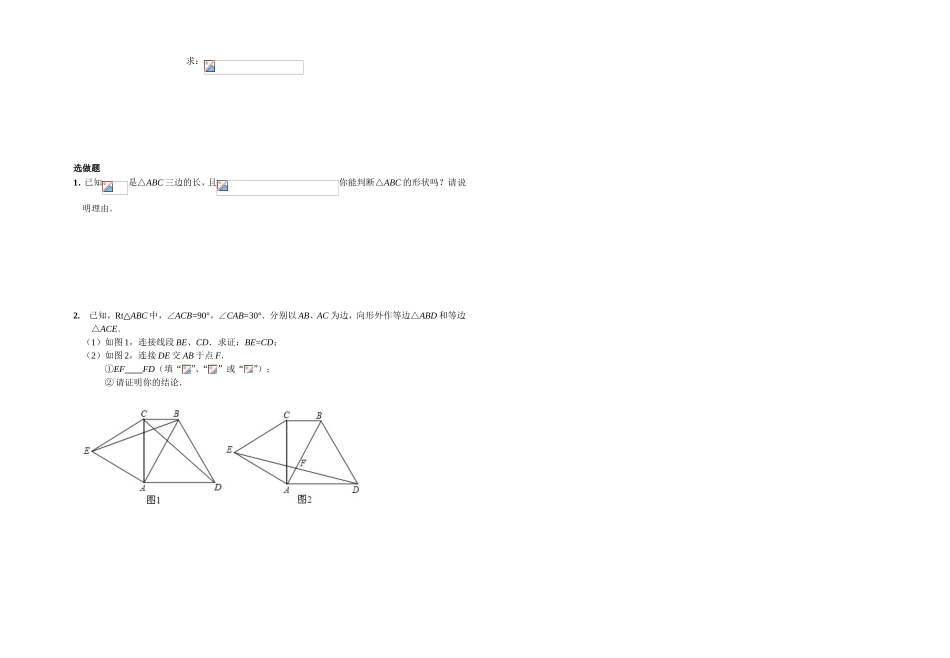
完全平方公式【学习目标】1.能熟练运用完全平方公式进行多项式的因式分解,培养学生观察分析能力.2.培养科学的质疑精神与积极地将新旧知识进行关联的倾向,以及学习数学的兴趣.【问题探究】(1);(2);完全平方式的特点:①项数必须是____________项;②其中有两项是___________________;③另一项是_________________________________.归纳得出:即两个数的平方和加上(或减去)这两个数的积的2倍,等于这两个数的和(或差)的平方.【示范引领1】例1.判断下列各式能运用完全平方公式分解因式吗?①a2-4a+4()②x2+4x+4y2()③4a2+2ab+b2()④a2-ab+b2()小结:1完全平方式的特点是:首末两项和是两个数的平方和的形式,而中间一项是这两数积的2倍.【课堂操练1】1.判断下列各式能运用完全平方公式分解因式吗?①x2-6x-9()②a2+a+0.25()③()④()2.分解因式:(口答)(1)=____________;(2)=____________;(3)=____________;(4)=____________;(5)=____________;(6)=____________;(7)=____________;(8)=____________.【示范引领2】例2分解因式(1);(2);(3);(4);小结:2.的直接应用.3.关键掌握公式的特点,牢记公式.【课堂操练2】分解因式:3.(1);(2);(3);(4).【示范引领3】例3把下列各式分解因式:(1);(2);(3);(4);小结:4.提取符号后可运用完全平方公式,关键是符号.5.先找出各项的公因式,提尽公因式后,再把括号内的多项式用公式进行分解,另外整体思想的应用.【课堂操练3】4.分解因式:(1);(2);(3);(4);【示范引领4】例4把下列各式分解因式:(1);(2);小结:6.可先观察式子的结构特点,必要时先进行整理,灵活运用各种方法进行因式分解,另外一定要分解到不好再分解为止.【课堂操练4】5.分解因式:(1);(2);(3);(4).课堂小结:1.理解完全平方公式的定义;2.能灵活运用完全平方公式法进行因式分解;3.注意因式分解结果的要求;作业布置:中午作业《新课程》家庭作业学案一张【课后巩固】1.填空:(1)()+=(-;(2)=;(3)=;(4)=(+5.2.将下列各式填上适当的项,使它成为完全平方式()的形式:(1);(2);(3);(4);(5);(6);3.(1)若是完全平方式,则数的值是.(2)已知,则.(3)已知,则=.4.把下列各式分解因式:(1);(2);(3);(4);(5);(6);(7);(8);(9);(10).5.利用因式分解进行计算:(1);(2);(3);(4)已知,,求:选做题1.已知是△ABC三边的长,且你能判断△ABC的形状吗?请说明理由.2.已知,Rt△ABC中,∠ACB=90°,∠CAB=30°.分别以AB、AC为边,向形外作等边△ABD和等边△ACE.(1)如图1,连接线段BE、CD.求证:BE=CD;(2)如图2,连接DE交AB于点F.①EFFD(填“”、“”或“”);②请证明你的结论.