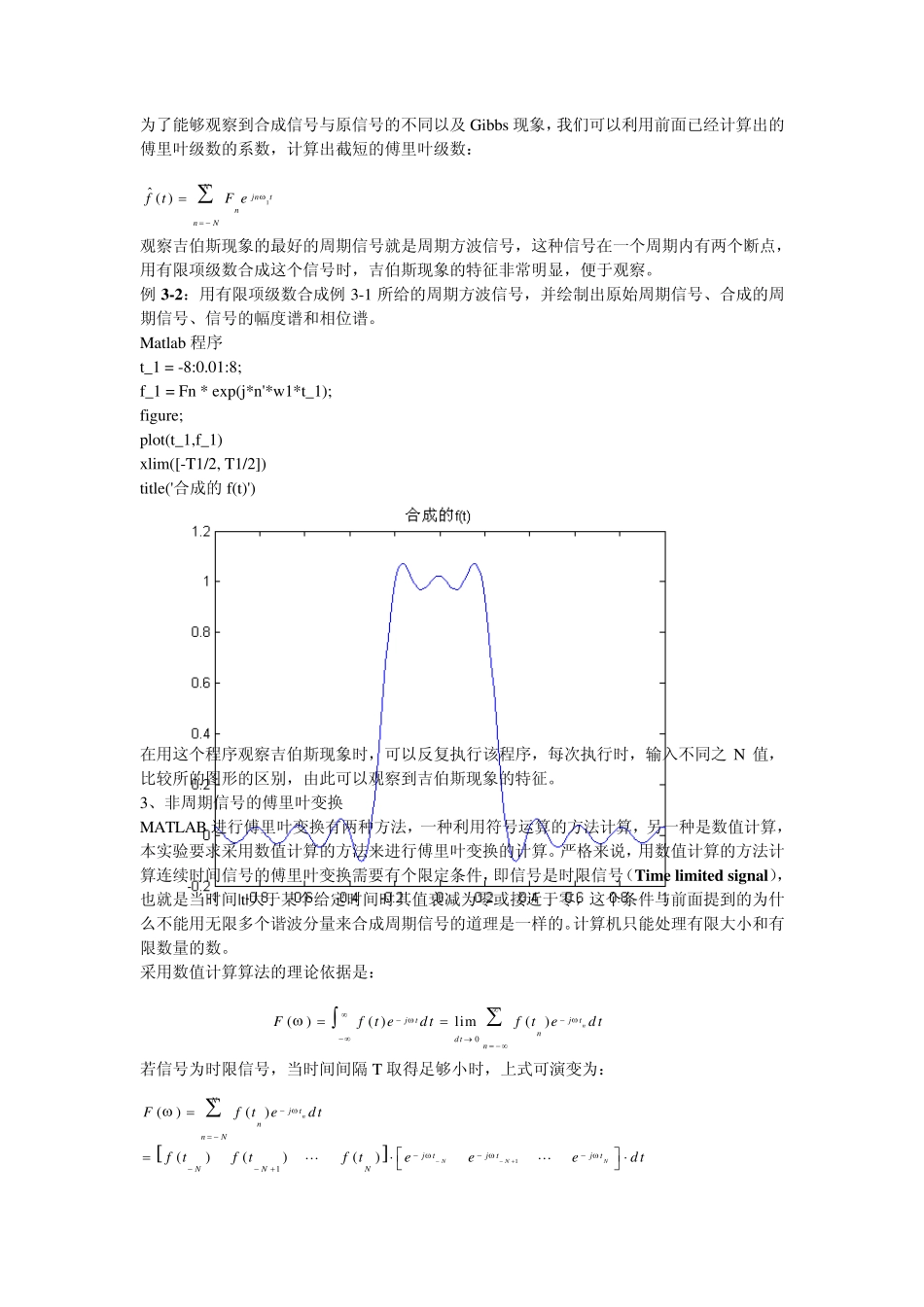
实验三 连续信号、系统的频域分析、复频域分析 一、实验目的 1、理解频域分析的MATLAB 实现方法。 2、求解系统的频率响应。 3、理解函数的拉氏变换,并进行复频域 二、实验时数: 2 学时 三、实验相关知识: (一)连续信号的频谱分析 1、周期信号的傅里叶级数计算 设周期信号x (t)的基本周期为T1,且满足狄里克利条件,则其指数形式的傅里叶级数系数Fn 为: 1112211( )TjntnTFft edtT 其中n 为-∞,∞之间的整数;角频率ω1=2π/T1。 因为计算机不能计算无穷多个系数,所以我们假设需要计算的谐波次数为N,则总的系数个数为2N+1 个。在确定了信号的周期T1 和时间步长 dt 之后,对某一个系数,上述系数的积分公式可以近似为: 11111 11 212211112111( )()()()()/kMMTjntjntnkTkTjntjntjntMFf t edtf tedtTTf tf tf teeedt T 对于全部需要的2N+1 个系数,上面的计算可以按照矩阵运算实现。需要强调的是,时间变量的变化步长 dt 的大小对傅里叶级数系数的计算精度的影响非常大,dt 越小,精度越高,但是,计算机计算所花的时间越长。 例 3-1:求如图所示方波信号的幅度谱,并画出频谱图。(A=1,τ =0.5,T1=2) tf(t)Aτ/2-τ/2T1/2-T1/2T1-T1 MATLAB 实现傅里叶级数计算的程序如下: dt = 0.01; T1 = 2; w1 = 2*pi/T1; t = -T1/2:dt:T1/2; tau = 0.5; A = 1; f = A*(u(t + tau/2) - u(t - tau/2)); subplot(2,1,1) plot(t,f) axis([-T1/2, T1/2, -0.1, 1.1]) title('f(t)时域波形') N = 10; n = -N:N; Fn = f*exp(-j*t'*w1*n)*dt/T1; subplot(2,1,2) stem(n,Fn) hold on dw = 0.01; w = -N*w1:dw:N*w1; F = A*tau/T1 * sinc(w*tau/2/pi); plot(w/w1,F,'--') title('傅里叶级数F_n') 2、周期信号的合成以及 Gibbs 现象 从傅里叶级数的合成式(Synthesis equation) 1( )jntnnf tF e 可以看出,用无穷多个不同频率和不同振幅的周期复指数信号可以合成一个周期信号。然而,我们无法用计算机实现对无穷多个周期复指数信号的合成。但是,用有限项来合成却是可行的,在实际应用中,多半也就是这么做的。然而,这样做的一个必然结果,就是引入了误差。 如果一个周期信号在一个周期有内断点存在,那么,引入的误差将除了产生纹波之外,还将在...