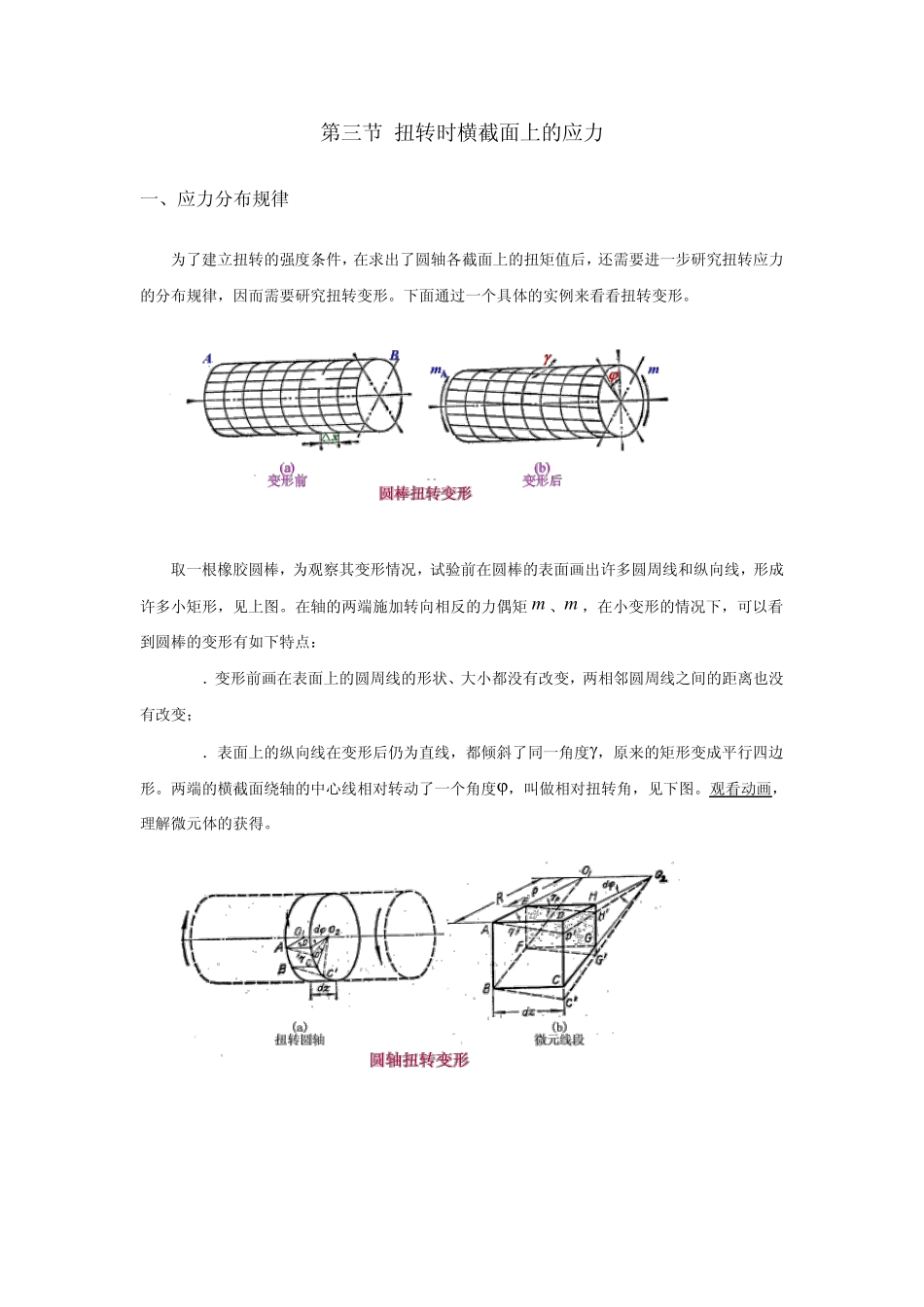
第三节 扭转时横截面上的应力 一、应力分布规律 为了建立扭转的强度条件,在求出了圆轴各截面上的扭矩值后,还需要进一步研究扭转应力的分布规律,因而需要研究扭转变形。下面通过一个具体的实例来看看扭转变形。 取一根橡胶圆棒,为观察其变形情况,试验前在圆棒的表面画出许多圆周线和纵向线,形成许多小矩形,见上图。在轴的两端施加转向相反的力偶矩 mA、mB,在小变形的情况下,可以看到圆棒的变形有如下特点: 1.变形前画在表面上的圆周线的形状、大小都没有改变,两相邻圆周线之间的距离也没有改变; 2.表面上的纵向线在变形后仍为直线,都倾斜了同一角度,原来的矩形变成平行四边形。两端的横截面绕轴的中心线相对转动了一个角度 ,叫做相对扭转角,见下图。观看动画,理解微元体的获得。 通过观察到的表面现象,可以推理得出以下结果: ★ 各横截面的大小、形状在变形前后都没有变化,仍是平面,只是相对地转过了一个角度,各横截面间的距离也不改变,从而可以说明轴向纤维没有拉、压变形,所以,在横截面上没有正应力产生; ★ 圆轴各横截面在变形后相互错动,矩形变为平行四边形,这正是前面讨论过的剪切变形,因此,在横截面上应有剪应力; ★ 变形后,横截面上的半径仍保持为直线,而剪切变形是沿着轴的圆周切线方向发生的。所以剪应力的方向也是沿着轴的圆周的切线方向,与半径互相垂直。 由此知道扭转时横截面上只产生剪应力,其方向与半径垂直。 下面进一步讨论剪应力在横截面上的分布规律。 为了观察圆轴扭转时内部的变形情况,找到变形规律,取受扭转轴中的微段 dx来分析(上图a)。假想O2DC 截面象刚性平面一样地绕杆轴线转动 d,轴表面的小方格ABCD 歪斜成平行四边形 ABC'D',轴表面 A 点的剪应变就是纵线歪斜的角,而经过半径 O2D 上任意点H 的纵向线 EH 在杆变形后倾斜了一个角度,它也就是横截面上任一点E 处的剪应变。应该注意,上述剪应变都是在垂直于半径的平面内的。设H 点到轴线的距离为 ,由于构件的变形通常很小,即 所以 (a) 由于截面 O2DC 象刚性平面一样地绕杆轴线转动,图上△O2HH'与△O2DD'相似,得 (b) 将式(b)代入(a)式得 (1-40) 上式表明,圆轴扭转时,横截面上靠近中心的点剪应变较小;离中心远的点剪应变较大;轴表面点的剪应变最大。各点的剪应变与离中心的距离成正比。 根据剪切虎克定律知道剪应力与剪应变成正比,即=G·。在弹性范...