机械优化设计复合型法

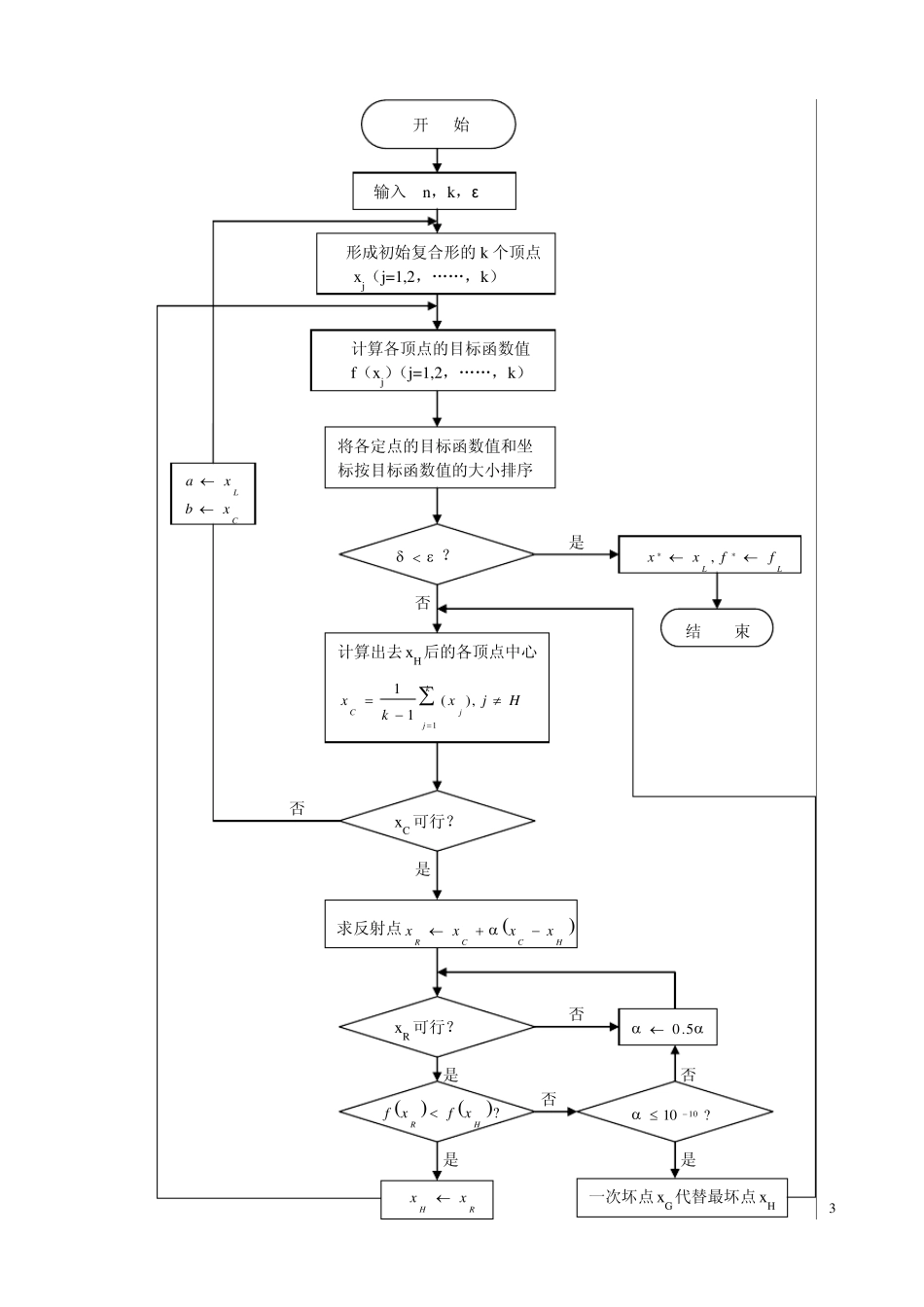
1 机械优化设计实验报告 2 (一 ) 题目：用复合形法求约束优化问题  2221645minxxxf；06422211xxg；01013 xg的最优解。 基本思路：在可行域中构造一个具有K 个顶点的初始复合形。对该复合形各顶点的目标函数值进行比较，找到目标函数值最大的顶点（即最坏点），然后按一定的法则求出目标函数值有所下降的可行的新点，并用此点代替最坏点，构成新的复合形，复合形的形状每改变一次，就向最优点移动一步，直至逼近最优点。 (二 ) 复合形法的计算步骤 1） 选择复合形的顶点数k， 一般取nkn21， 在可行域内构成具有k 个顶点的初始复合形。 2） 计算复合形个顶点的目标函数值，比较其大小，找出最好点xL、最坏点xH、及此坏点xG.. 3） 计算除去最坏点xH以外的（k-1）个顶点的中心xC。判别xC是否可行，若xC为可行点，则转步骤4）；若xC为非可行点，则重新确定设计变量的下限和上限值，即令CLxbxa,，然后转步骤1），重新构造初始复合形。 4） 按式HCCRxxxx计算反射点xＲ ，必要时改变反射系数α 的值，直至反射成功，即满足式HRRjxfxfmjxg;,2,1,0，。然后xＲ 以取代xＨ ，构成新的复合形。 5） 若收敛条件  211211kjLjxfxfk得到满足，计算终止。约束最优解为： LLxfxfxx*,*。 (三 ) 复合形法程序框图见下图： 3 开 始 输入 n ，k ，ε 形成初始复合形的k 个顶点 x j（j=1,2，……，k ） 将各定点的目标函数值和坐 标按目标函数值的大小排序 计算出去 x H后的各顶点中心 HjxkxkjjC,)(111  ？ x C 可行？ x R 可行？ 结 束 一次坏点x G代替最坏点x H 计算各顶点的目标函数值 f（x j）（j=1,2，……，k ） 求反射点HCCRxxxx RHxx ?HRxfxf 5.0 ?1010 CLxbxa LLffxx**, 否 是 是 是 是 否 否 否 否 是 4 (四) 源程序如下： #include double objfx(double x[]) { double ff; ff=(x[0]-5)*(x[0]-5)+4*(x[1]-6)*(x[1]-6); return ff; } #include void main() { void comple(int n,int k,int kg,double ep,double x[],double bl[],double bu[], double xcom[][100],double *f) ; double a[]={0,0},b[]={10,20},...