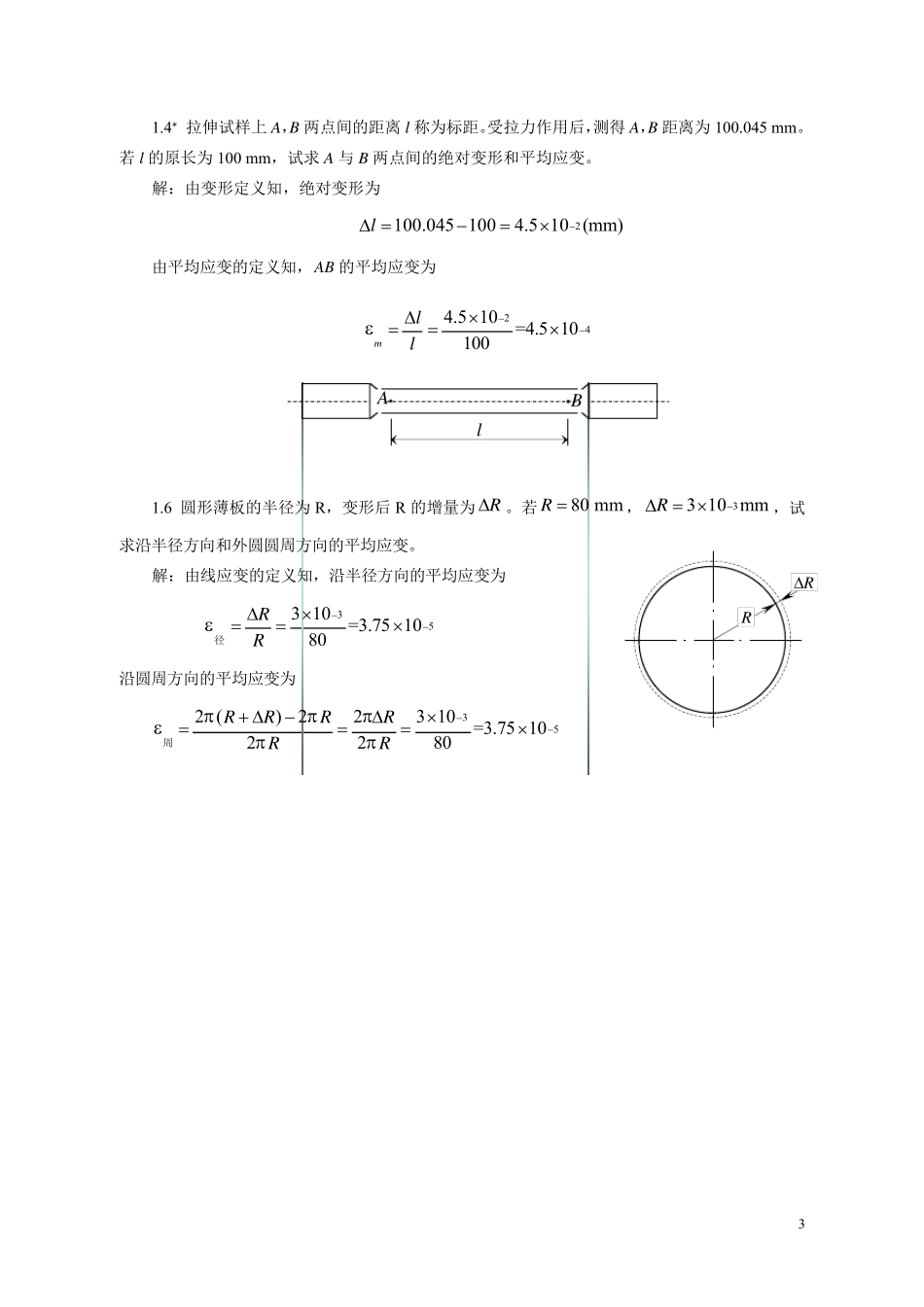
1ABCnnmm1 m1 m1 m3 kN(a) NFABnnmm1 m1 m1 m3 kN(b)NFOBnnmm1 m1 m3 kNSFM(c) 1.2 试求图示结构m-m 和n-n 两截面上的内力,并指出AB 和BC 两杆的变形属于哪一类基本变形。 解: 一、应用截面法,取 n-n 截面以下部分为研究对象,受力图如(b),由平衡条件 A=0M∑,N33 20F × − ×= 得 N2kNF = BC 杆的变形属于拉伸变形。 二、应用截面法,取 m-m 截面以右,n-n 截面以下部分为研究对象,受力图如(c),由平衡条件 O=0M∑,N23 10FM× − × −= 得 1 kN mM =⋅ =0yF∑,SN30FF− += 得 S1 kNF = AB 杆的变形属于弯曲变形。 1.3 在图示简易吊车的横梁上,F 力可以左右移动。试求截面1-1 和2-2 上的内力及其最大值。 解: 应用截面法,取 1-1 截面右侧部分为研究对象,受力图如(b),由平衡条件 A=0M∑,N1 sin0FlF xα⋅⋅ −⋅= (1) 得 N1sinF xFlα⋅= ⋅ 因 x 的变化范围为0xl≤≤ ,所以当 xl=时,N1F达到最大值,即 N1sinFFα= 2αBCA11lx22F(a) αBA11lxFN1F(b)αB112FN1F2MN2FS2FO(c) 应用截面法,取图(a)所示1-1 和2-2 截面以右部分为研究对象,受力图如图(c),由平衡条件 =0xF∑,N2N1 cos0FFα−⋅= (2) =0yF∑,S2N1 sin0FFFα−+⋅= (3) O=0M∑,N12sin()0FlxMα⋅⋅−−= (4) 解以上各式,得 N2cot/Fx Flα=⋅⋅,S2(1/ )Fx l F=−,2()/MlxF x l=−⋅ 当x l=时,FN2 达到最大值,即 N2maxcotFFα=⋅ 当0x=时,FS2 达到最大值,即 S2maxFF= 当/ 2x l=时,M2 达到最大值,即 2max/ 4MF l=⋅ 1.4 拉伸试样上A,B 两点间的距离l 称为标距。受拉力作用后,用变形仪量出两点间的距离为24.5 10 mml−Δ =×。若 l 的原长为100 mm,试求 A 与 B 两点间的平均应变mε 。 解:由平均应变的定义知,AB 的平均应变为 244.5 10=4.5 10100mllε−−Δ×==× ABl 31.4* 拉伸试样上A,B 两点间的距离l 称为标距。受拉力作用后,测得 A,B 距离为100.045 mm。若 l 的原长为100 mm,试求 A 与 B 两点间的绝对变形和平均应变。 解:由变形定义知,绝对变形为 2100.045 1004.5 10 (mm)l−Δ =−=× 由平均应变的定义知,AB 的平均应变为 244.5 10=4.5 10100mllε−−Δ×==× 1.6 圆形薄板的半径为R,变形后 R 的增量为RΔ。若80 mmR =,33 10 ...