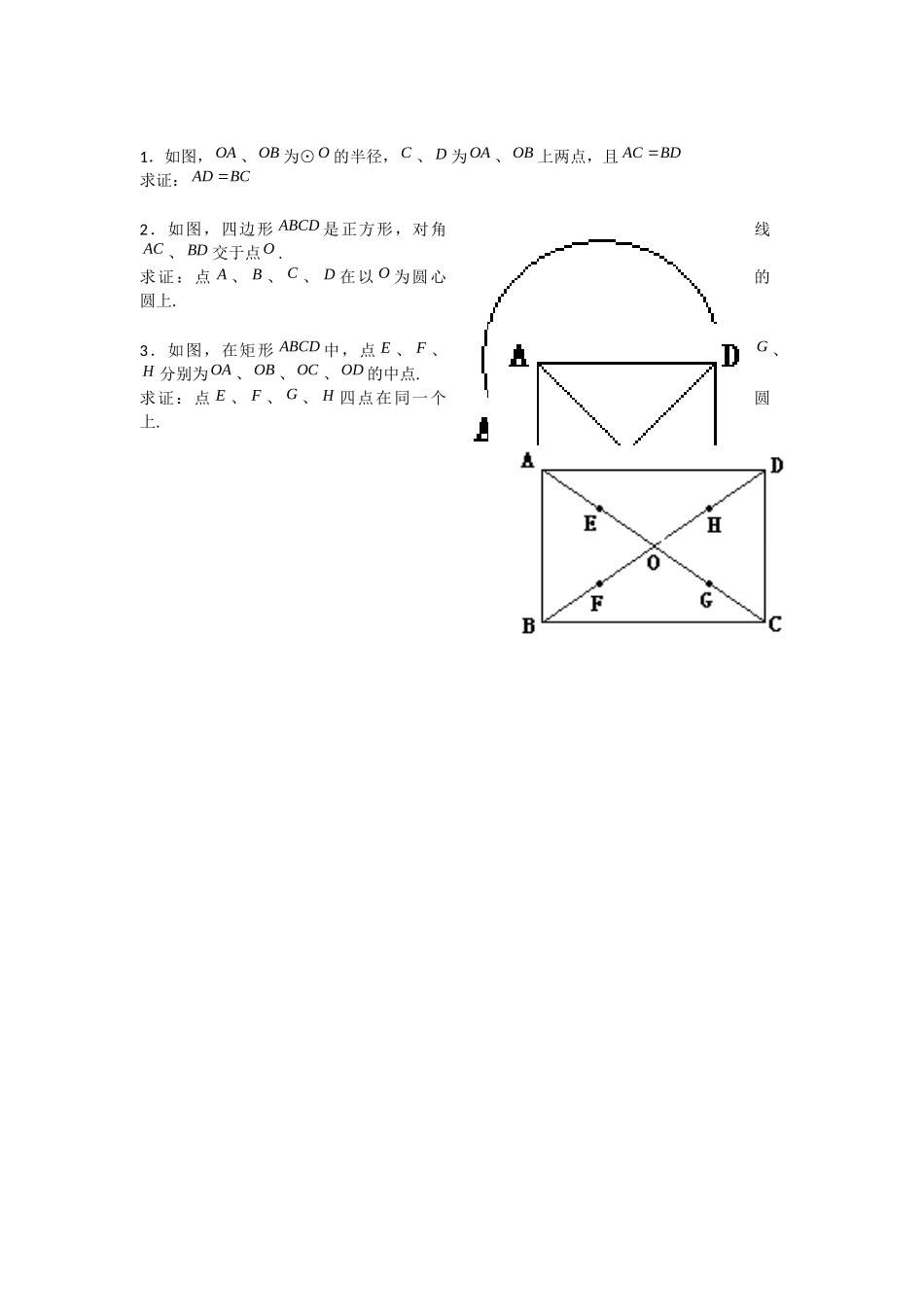
《圆》第一节 圆导学案 1主编人: 主审人:班级: 学号: 姓名: 学习目标:【知识与技能】理解圆的定义及弧、弦、半圆、直径等相关概念。【过程与方法】经历动手实践、观察思考、分析概括的学习过程,养成自主探究、合作沟通的良好习惯。【情感、态度与价值观】利用我国悠久的数学讨论历史,对学生进行爱国主义熏陶;通过圆的完美性,让学生进行美的体验。【重点】与圆有关的概念【难点】圆的概念的理解学习过程:一、自主学习(一)复习巩固1、举出生活中的圆的例子 2、圆既是 对称图形,又是 对称图形。3、圆的周长公式 C= 圆的面积公式 S= (二)自主探究1、圆的定义:在一个平面内,线段 OA 绕它固定的一个端点 O 旋转 ,另一个端点所形成的图形叫做 .固定的端点 O 叫做 ,线段 OA 叫做 .以点 O 为圆心的圆,记作“ ”,读作“ ” 决定圆的位置, 决定圆的大小。圆的定义:到 的距离等于 的点的集合.2、弦:连接圆上任意两点的 叫做弦 直径:经过圆心的 叫做直径3、弧: 任意两点间的部分叫做圆弧,简称弧半圆:圆的任意一条 的两个端点把圆分成两条弧,每一条 都叫做半圆优弧: 半圆的弧叫做优弧。用 个点表示,如图中 叫做优弧劣弧: 半圆的弧叫做劣弧。用 个点表示,如图中 叫做劣弧等圆:能够 的两个圆叫做等圆等弧:能够 的弧叫做等弧4、 假如四边形 ABCD 是矩形,它的四个顶点在同一个圆上吗?假如在,这个圆的圆心在哪里?5、 已知:如图,在⊙中,AB,CD 为直径求证:(三)、归纳总结: 1、在平面内任意取一点 P,点与圆有哪几种位置关系?若⊙O 的半径为 r,OCABOCABDOBCAD //点 P 到圆心 O 的距离为 d,那么:点 P 在圆 d r 点 P 在圆 d r 点 P 在圆 d r2、圆的集合定义(集合的观点)(1)思考:平面上的一个圆把平面上的点分成哪几部分? (2)圆的内部是到 的点的集合;圆的外部是 的点的集合 。(四)自我尝试:1、如何在操场上画一个半径是 5m 的圆?说出你的理由。2、你见过树木的年轮吗?从树木的年轮,可以很清楚的看出树木生长的年轮。把树木的年轮看成是圆形的,假如一棵 20 年树龄的红杉树的树干直径是 23cm,这棵红杉树的半径平均每年增加多少?二、老师点拔 1、圆心决定圆的 ,而半径决定圆的 ;直径是圆中经过 的特别的弦,是 的弦,并且等于 的 2 倍,是在讨论圆的问题中出现次数最多的重要线段但弦不一定是直径,...