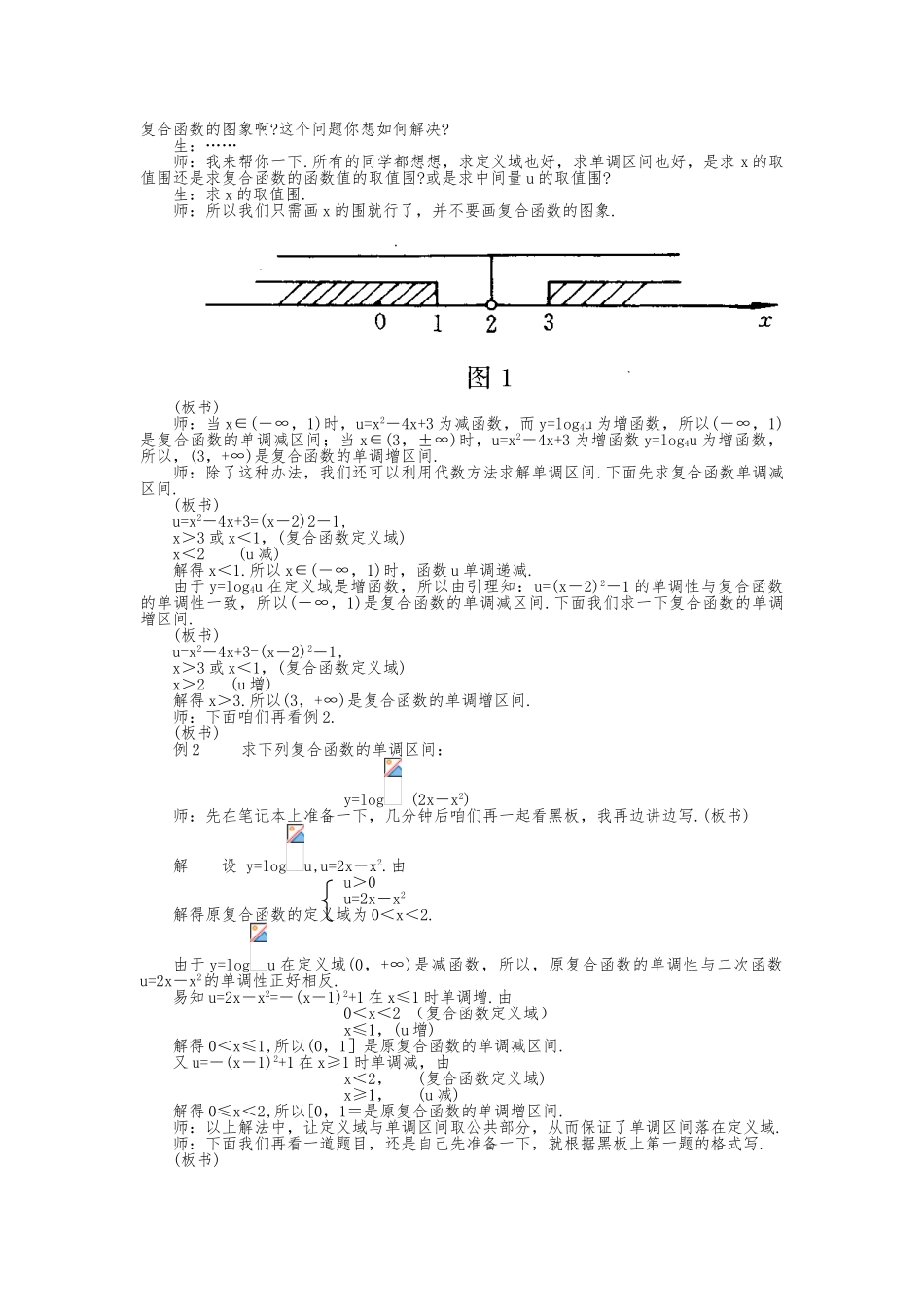
课题:函数的单调性(二)复合函数单调性二十二中 青教学目标1.掌握有关复合函数单调区间的四个引理.2.会求复合函数的单调区间.3.必须明确复合函数单调区间是定义域的子集.教学重点与难点1.教学重点是教会学生应用本节的引理求出所给的复合函数的单调区间.2.教学难点是务必使学生明确复合函数的单调区间是定义域的子集.教学过程设计师:这节课我们将讲复合函数的单调区间,下面我们先复习一下复合函数的定义.生 : 设 y=f(u) 的 定 义 域 为 A , u=g(x) 的 值 域 为 B , 若 AÍB , 则 y 关 于 x 函 数 的y=f[g(x)]叫做函数 f 与 g 的复合函数,u 叫中间量.师:很好.下面我们再复习一下所学过的函数的单调区间.(老师把所学过的函数均写在黑板上,中间留出写答案的地方,当学生回答得正确时,由老师将正确答案写在对应题的下边.)(老师板书,可适当略写.)例 求下列函数的单调区间.1.一次函数 y=kx+b(k≠0).解 当 k>0 时,(-∞,+∞)是这个函数的单调增区间;当 k<0 时,(-∞,+∞)是这个函数的单调减区间.2.反比例函数 y=(k≠0).解 当 k>0 时,(-∞,0)和(0,+∞)都是这个函数的单调减区间,当 k<0 时,(-∞,0)和(0,+∞)都是这个函数的单调增区间.3.二次函数 y=ax2+bx+c(a≠0).解 当 a>1 时(-∞,-)是这个函数的单调减区间,(-,+∞)是它的单调增区间;当 a<1 时(-∞,-)是这个函数的单调增区间,(-,+∞)是它的单调减区间;4.指数函数 y=ax(a>0,a≠1).解 当 a>1 时,(-∞,+∞)是这个函数的单调增区间,当 0<a<1 时,(-∞,+∞)是这个函数的单调减区间.5.对数函数 y=logax(a>0,a≠1).解 当 a>1 时,(0,+∞)是这个函数的单调增区间,当 0<a<1 时,(0,+∞)是它的单调减区间.师:我们还学过幂函数 y=xn(n 为有理数),由于 n 的不同取值情况,可使其定义域分几种情况,比较复杂,我们不妨遇到具体情况时,再具体分析.师:我们看看这个函数 y=2x2+2x+1,它显然是复合函数,它的单调性如何?生:它在(-∞,+∞)上是增函数.师:我猜你是这样想的,底等于 2 的指数函数为增函数,而此函数的定义域为(-∞,+∞),所以你就得到了以上的答案.这种做法显然忽略了二次函数 u=x2+2x+1 的存在,没有考虑这个二次函数的单调性.咱们不难猜想复合函数的单调性应由两个函数共同决定,但一时猜不准结论.下面我们引出并证明一些有关的预备定理.(板书)引...