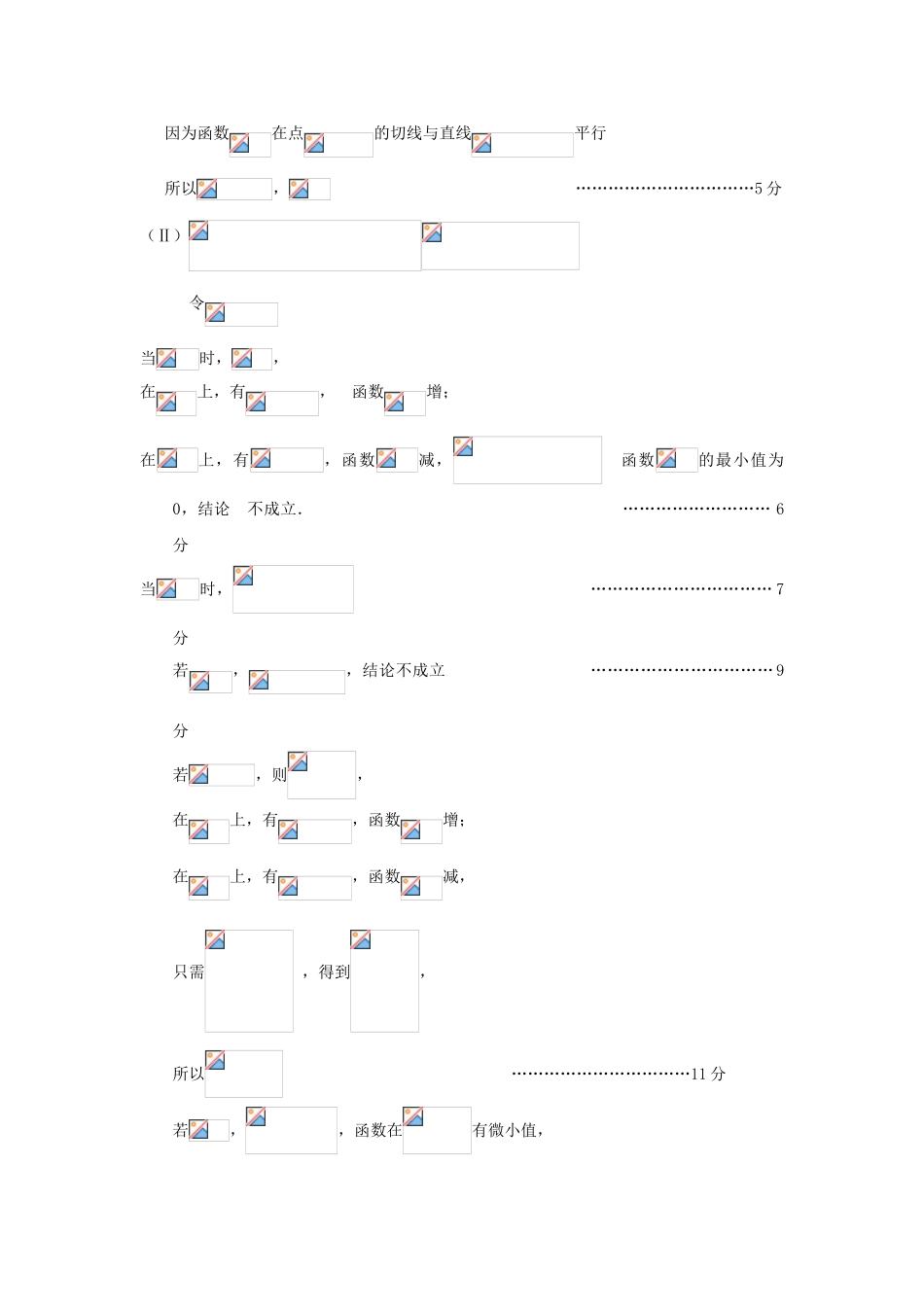
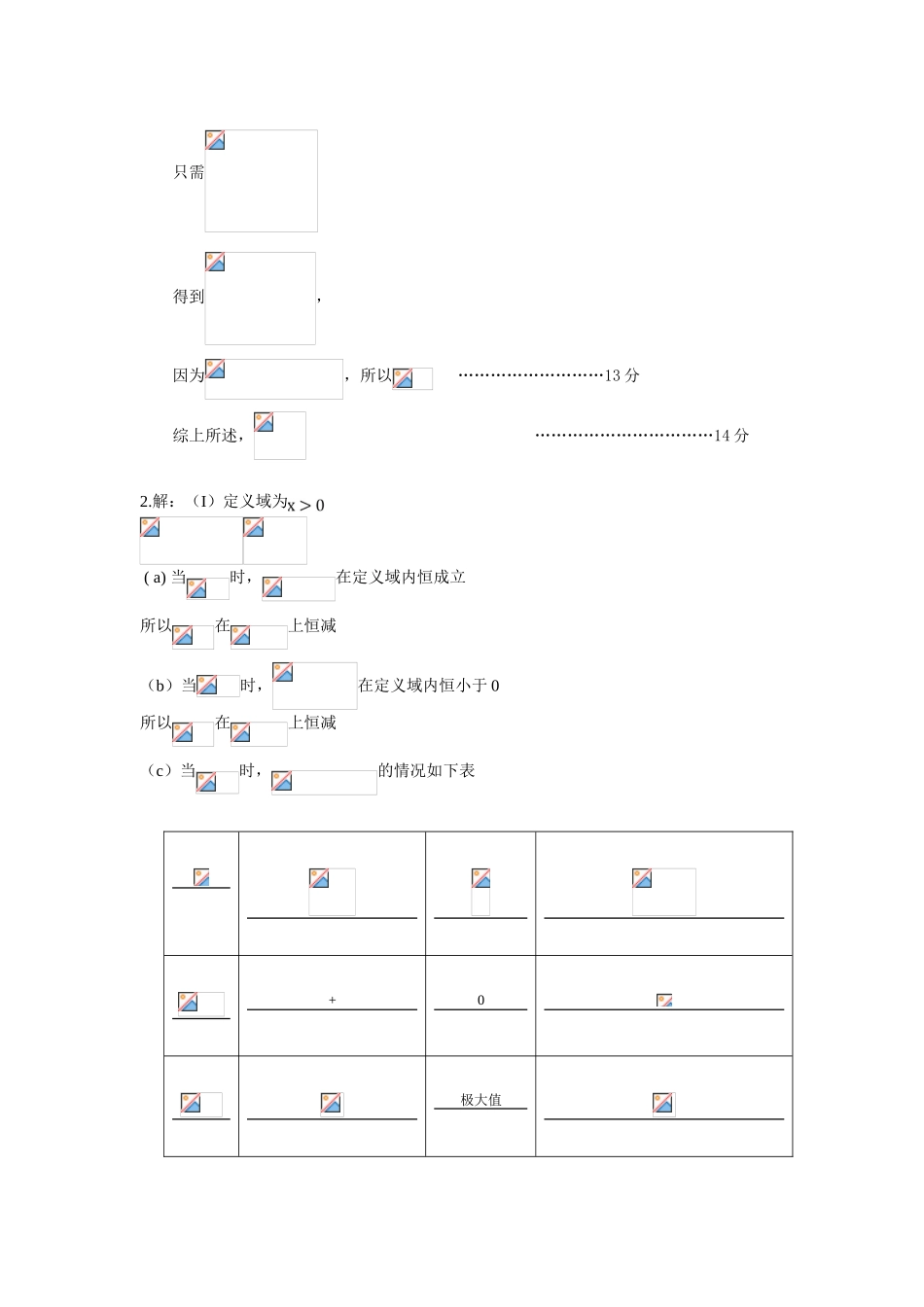
导数 31.已知函数.(Ⅰ)函数在点处的切线与直线平行,求的值;(Ⅱ)当时,恒成立,求的取值范围.2.已知函数 f(x)=ax-1-1n x,aR.(I)讨论函数 f(x)的单调区间:(II)若函数 f(x)在 x=l 处取得极值,对x∈(0,+),f(x)≥bx-2 恒成立,求实数 b 的取值范围.3.已知函数 ,. (Ⅰ)当时,求曲线在点处的切线方程;(Ⅱ)求函数的单调区间;(Ⅲ)当时,函数在上的最大值为,若存在,使得成立,求实数 b 的取值范围.答案1.解: (Ⅰ) ……………………………2分, ……………………………3分 因为函数在点的切线与直线平行所以, ……………………………5 分(Ⅱ)令当时,,在上,有, 函数增;在上,有,函数减, 函数的最小值为0,结论 不成立. ……………………… 6分当时, …………………………… 7分若,,结论不成立 …………………………… 9分若,则,在上,有,函数增;在上,有,函数减,只需 ,得到,所以 ……………………………11 分若,,函数在有微小值,只需得到,因为,所以 ………………………13 分综上所述, ……………………………14 分2.解:(I)定义域为 ( a) 当时,在定义域内恒成立所以在上恒减(b)当时,在定义域内恒小于 0所以在上恒减(c)当时,的情况如下表+0极大值所以在为增函数,在为减函数综上:当时,在定义域上恒减当时,在为增函数,在为减函数(II)由(I)可得,当时,在定义域上无极值,当时,在处取得极值,所以,解得所以 ,即解得令,易得在上递减,在上递增。所以;即:3.解:(Ⅰ)当时,……………………1 分………………………………………….…2 分所以曲线在点处的切线方程…………………………….…3 分(Ⅱ)………4 分① 当时,解,得,解,得所以函数的递增区间为,递减区间为在………………………5 分②时,令得或i)当时,………………………6 分函数的递增区间为,,递减区间为……………………7 分当时,,所以恒大于 0所以在上恒增ii)当时,在上,在上………………………8 分函数的递增区间为,递减区间为………………………9 分(Ⅲ)由(Ⅱ)知,当时,在上是增函数,在上是减函数,所以,…………………………………11 分存在,使即存在,使,将整理得从而有所以的取值范围是. …………………………13 分x)f’(x)+0-0+f(x)增极大减微小增更多试题下载: (在文字上按住 ctrl 即可查看试题)高考模...