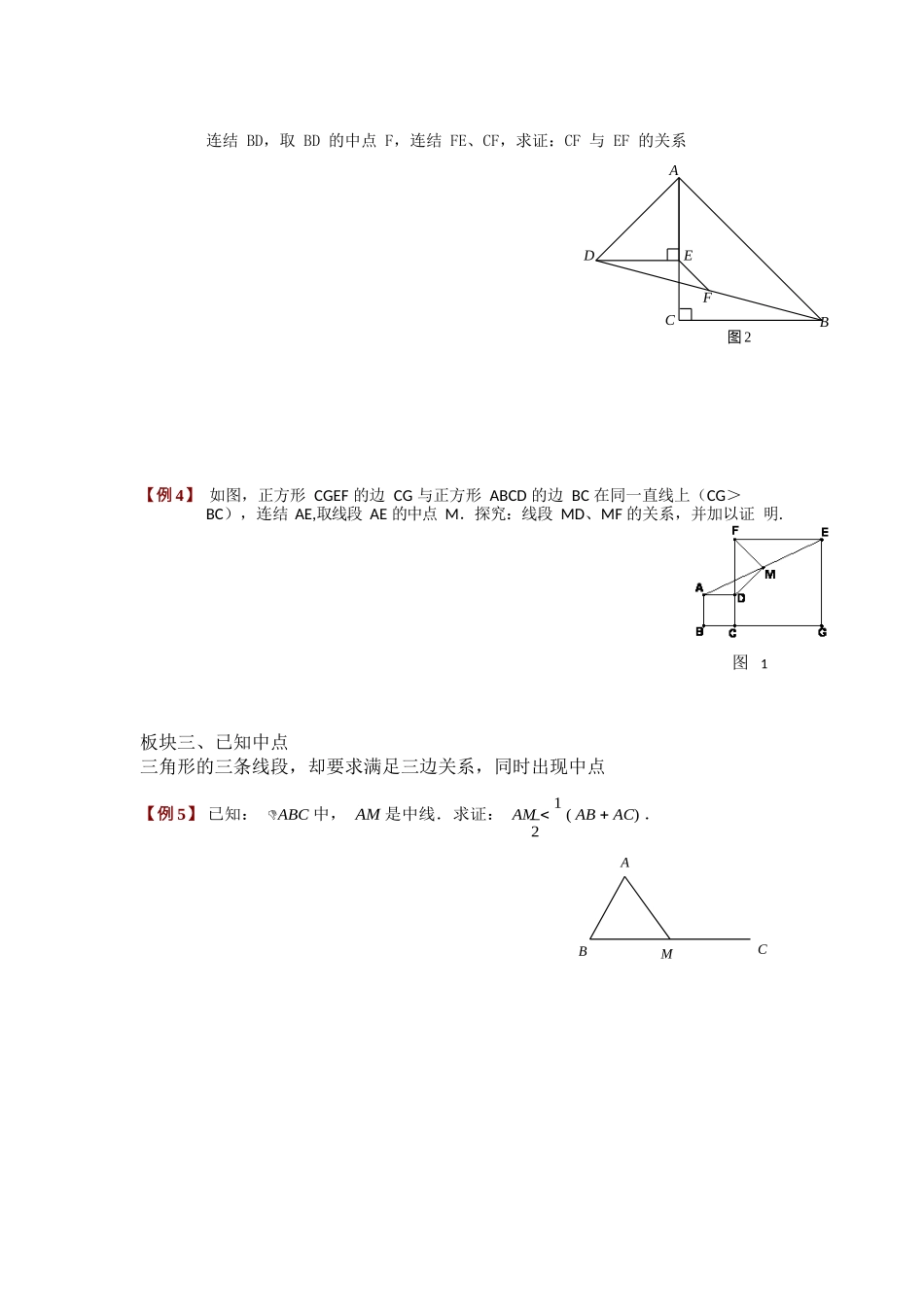
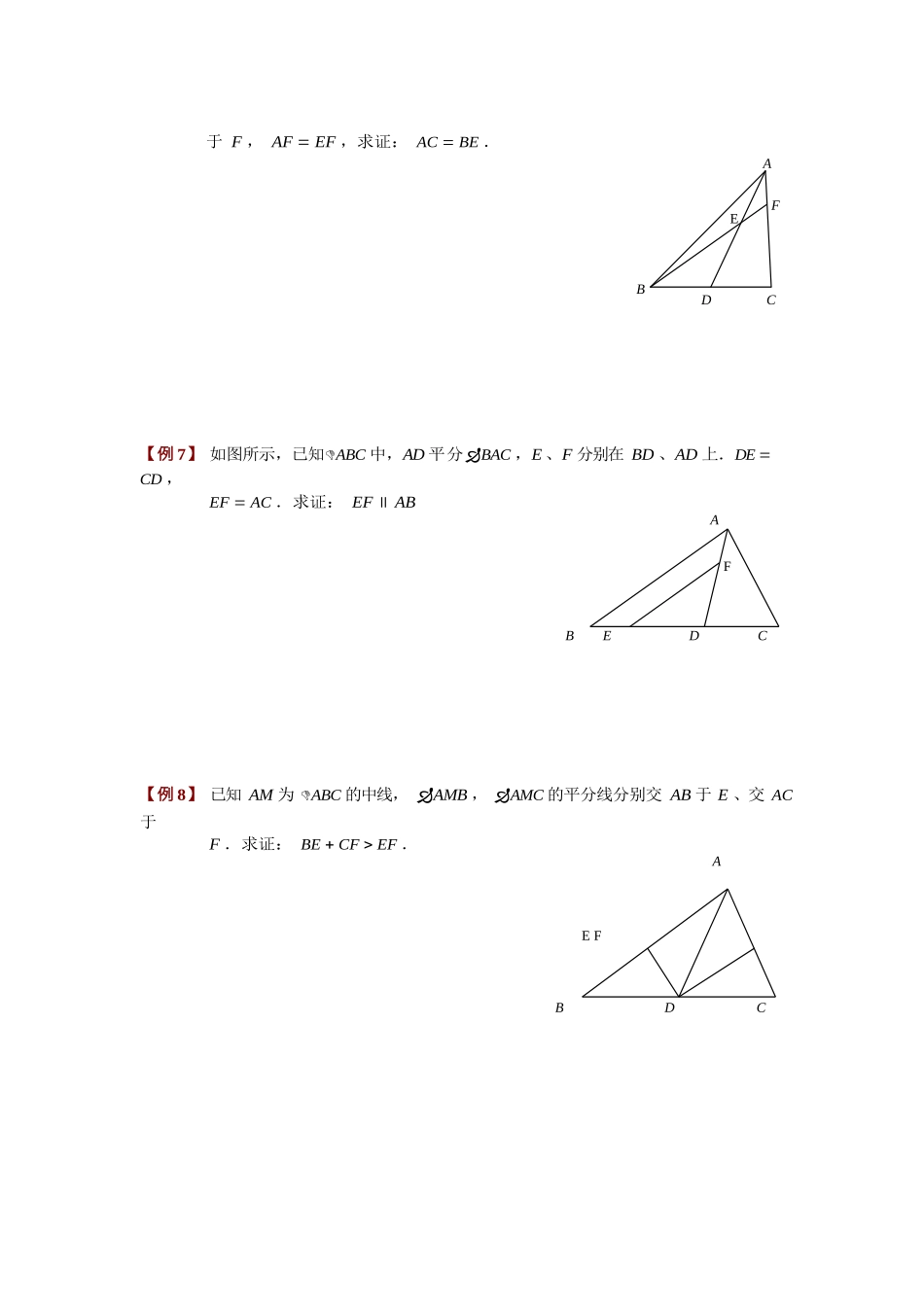
DEEA BC倍长中线它延续着旋转的思想,它们都是把离散的条件集中起来,构成新的图形,从而产生新的已知条件。已知在△ ABC 中, AD 是 BC 上的中线,延长 AD 至 E ,使 DE AD ,这样会产生 ACD 辅助线的叙述有EBD 、ACBE ,实质上,相当于把 ACD 中心旋转一下,所以○1 延长:延长 AD 至 E ,使 DE AD (通常已知中点)○2 作平行:过 B 作 BE AC 交 AD 延长线于 E (通常用于求证中点)板块一、平行线间出现中点【例 1】 如图,在正方形 ABCD 中, F 是 CD 的中点, E 是 BC 边上的一点,且 AF 平分DAE ,求证: AE EC CDADFBEC【例 2】 如图,梯形 ABCD 中, AB∥DC , E 是 AD 的中点.⑴ 当 AB 、 DC 、 BC 满足什么关系时, BE CE ?⑵ 若 BC AB DC ,是否有 BE CE ?⑶ 当 BC AB DC 时, ABE 、CBE 满足什么关系?⑷ 若DCE BCE , AB 、 DC 、 BC 满足何种关系?B ACD图 1连结 BD,取 BD 的中点 F,连结 FE、CF,求证:CF 与 EF 的关系ADEFCB图 2【例 4】 如图,正方形 CGEF 的边 CG 与正方形 ABCD 的边 BC 在同一直线上(CG>BC),连结 AE,取线段 AE 的中点 M.探究:线段 MD、MF 的关系,并加以证 明.板块三、已知中点三角形的三条线段,却要求满足三边关系,同时出现中点【例 5】 已知: ABC 中, AM 是中线.求证: AM 1 ( AB AC) .2ABMCEFE F于 F , AF EF ,求证: AC BE .AFBDC【例 7】 如图所示,已知ABC 中,AD 平分BAC ,E 、F 分别在 BD 、AD 上.DE CD ,EF AC .求证: EF ∥ ABA BEDC【例 8】 已知 AM 为 ABC 的中线, AMB , AMC 的平分线分别交 AB 于 E 、交 AC 于F .求证: BE CF EF .A BDCDB GCADCFBPEMQ连接 CE 、CD ,求证 CD 2EC .板块三、求证中点【例 10】已知ACB ,B ACB ,D ,E 分别是 AB 及 AC 延长线上的一点,且 BD CE , 连接 DE 交底 BC 于 G ,求证 GD GE .AE【例 11】已知△ABC 中,过 AB 边和 BC 边在三角形外分别作正方形 ABEF 和正方形 BCPQ, 连接 EQ,过 B 点作 BM⊥EQ,延长 MB 与 AC 交于 D 点,求证:D 是 AC 中点.