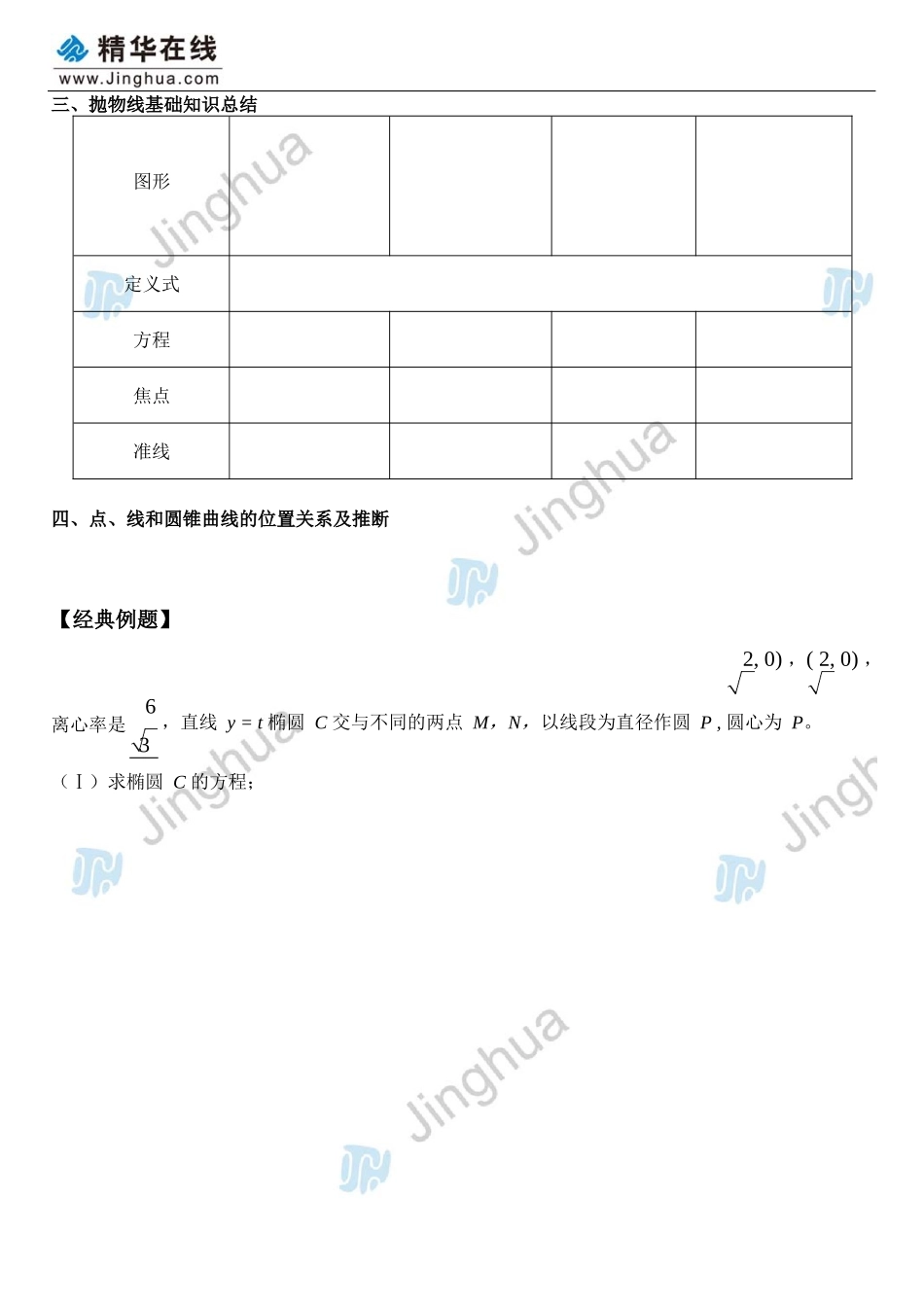
网络课程 内部讲义抛物线教 师:司马红丽爱护环境,从我做起,提倡使用电子讲义“”→ 在线名师资料室 免费资料任你下载第八讲 抛物线【知识要点归纳】一、椭圆和双曲线的基础知识总结椭圆双曲线图形定义式标准方程a, b, c 关系离心率及范围二、双曲线的特有性质1、双曲线的渐近线方程是 和 2、共渐近线的双曲线系方程为 3、等轴双曲线的方程为 , 等轴双曲线的性质(1)渐近线方程为 ,(2)渐近线互相 ,(3)离心率为 。三、抛物线基础知识总结图形定义式方程焦点准线四、点、线和圆锥曲线的位置关系及推断【经典例题】2, 0) ,( 2, 0) ,离心率是6 ,直线 y = t 椭圆 C 交与不同的两点 M,N,以线段为直径作圆 P , 圆心为 P。3(Ⅰ)求椭圆 C 的方程;5“”→ 在线名师资料室 免费资料任你下载右焦点的双曲线 C 的离心率 e .2(Ⅰ)求双曲线 C 的标准方程及其渐近线方程;例 3:根据条件,求抛物线标准方程(1)焦点坐标为 F 0, 2(2)抛物线的准线为 x 14(3)焦点到准线的距离等于 2(4)已知抛物线的顶点在原点,对称轴为 x 轴,抛物线上的点 M(-3,m)到焦点的距离等于 5, 求抛物线的方程和 m 的值.例 4:求解下列问题A. 4B. 6C. 8D. 12为垂足,假如直线 AF 斜率为 3 ,那么 PF A. 4 3B. 8C. 8 3D. 16(3)(2024 四川卷)已知直线 l1: 4x 3y 6 0 和直线l2: x 1,抛物线 y2 4x 上一动点 P 到直线 l1 和直线 l2 的距离之和的最小值是()1137A. 2B. 3C.D.516x 2例 5:已知直线 y = kx + 3 与椭圆2点、一个交点和没有交点。 y 2 1 ,试推断 k 的取值范围,使得直线与椭圆分别有两个交例 6:直线 y- kx-1 = 0 与椭圆 x5y21 恒有公共点,则 m 的取值范围是 m2y x“”→ 在线名师资料室 免费资料任你下载x2 221 的两焦点为 F , F ,点 P(x , y ) 满足 0 0 y 1 ,2120020则| PF |+ PF |的取值范围为 ,直线 x0 x y y 1 与椭圆 C 的公共点个数 。1220【课堂练习】1.A. 1B. 2C. 4D. 82.3.()1A.B. 1C. 2D. 424. 点 M 是抛物线 y2 12x 上的一点,且点 M 的横坐标为 5,则 M 到焦点的距离是 x2 y25.a2 1(a 0, b 0) 的一条渐近线方程是 y b23x ,它的一...