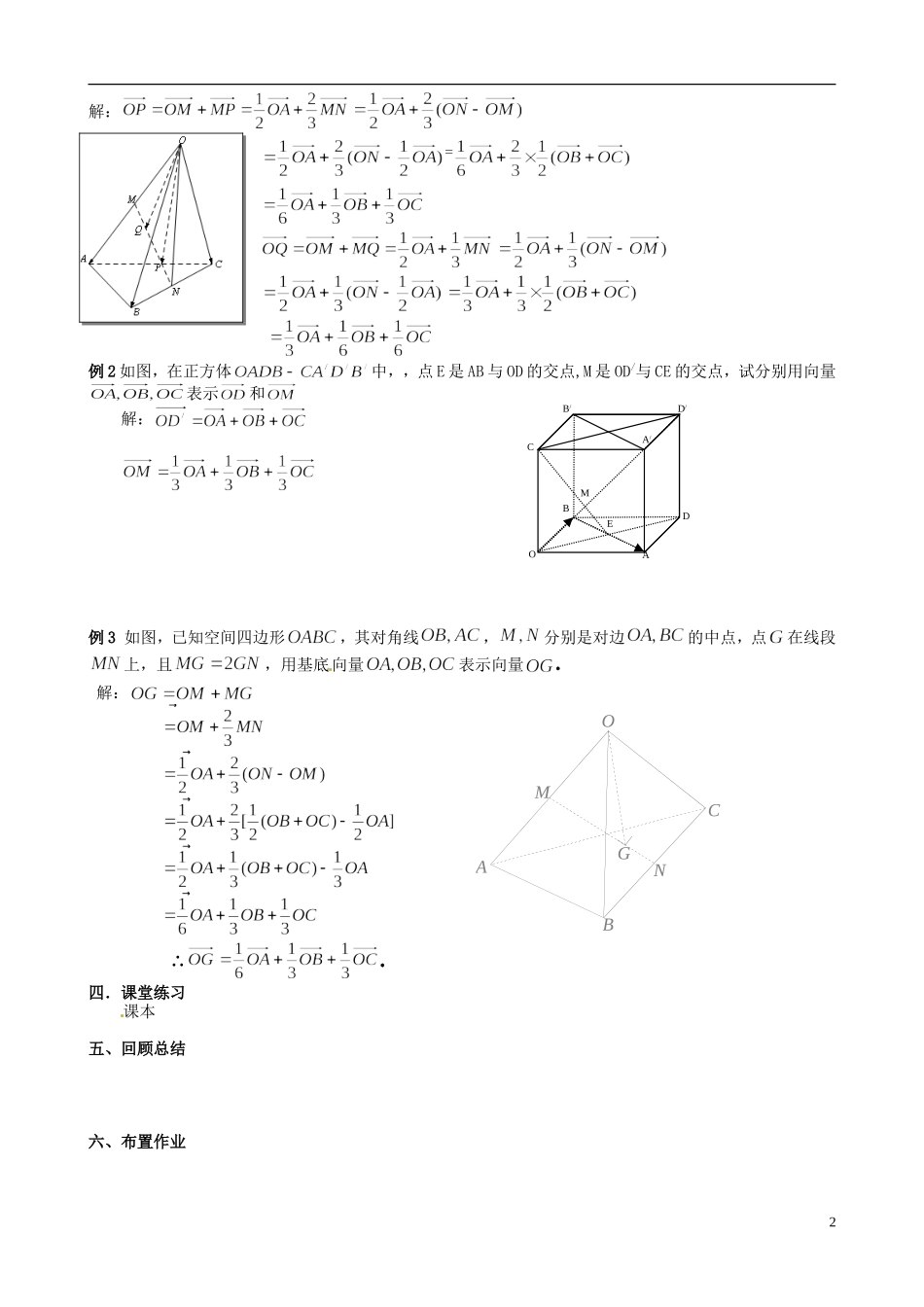
1e2eaPOA'P'B'C'BAC海南省保亭中学高中数学选修 2-1 教案:§3.1.4 空间向量的正交分解及其坐标表示课 题:空间向量的基本定理教学目标:1.掌握及其推论,理解空间任意一个向量可以用不共面的三个已知向量线性表示,而且这种表示是唯一的;2.在简单问题中,会选择适当的基底来表示任一空间向量。教学重点:空间向量的基本定理及其推论教学难点:空间向量的基本定理唯一性的理解教学过程:一、创设情景平面向量基本定理的内容及其理解如果是同一平面内的两个不共线向量,那么对于这一平面内的任一向量 ,有且只有一对实数,使 二、新课讲授1、空间向量的基本定理如果三个向量不共面,那么对空间任一向量,存在一个唯一的有序实数组,使证明:(存在性)设不共面,过点作过点作直线平行于,交平面于点;在平面内,过点作直线,分别与直线相交于点,于是,存在三个实数,使∴所以(唯一性)假设还存在使∴∴不妨设即 ∴∴共面此与已知矛盾 ∴该表达式唯一综上两方面,原命题成立奎屯王新敞新疆(注:上述证明不须给学生讲授)由此定理, 若三向量不共面,那么空间的任一向量都可由线性表示,所有空间向量组成的集合就是,这个集合可看作是由向量生成的,我们把{}叫做空间的一个基底,叫做基向量。注:空间任意三个不共面的向量都可以构成空间的一个基底奎屯王新敞新疆如果空间一个基底的三个基向量两两互相垂直,那么这个基底叫做正交基底.特别地,设、 、 为由公共起点的三个两两互相垂直单位向量,称这个基底为单位正交基底,以 、、 的公共起点为原点,分别以、 、 的方向为 轴、 轴、 轴的正方向建立空间直角坐标系。那么,对于空间任意一个向量,一定可以把它平移,使它的起点与原点重合,得到向量。有空间向量基本定理可知,存在有序实数组,使得,我们把称作向量在单位正交基底、、下的坐标,记作推论:设是不共面的四点,则对空间任一点,都存在唯 一的三个有序实数,使奎屯王新敞新疆有空间向量定理可知,空间任意一个向量都可以用不共面的向量表示出来,这能为解决问题带来方便。三、典例分析例 1 (课本例 4)如图,、 分别是四面体的边、的中点, 、 是的三等分点。用向量、、表示和。1OA/CMED/B/ADBABCOMNG解:= 例 2 如图,在正方体中,,点 E 是 AB 与 OD 的交点,M 是 OD/与 CE 的交点,试分别用向量表示和解:例 3 如图,已知空间四边形,其对角线,分别是对边的中点,点在线段上,且,用...