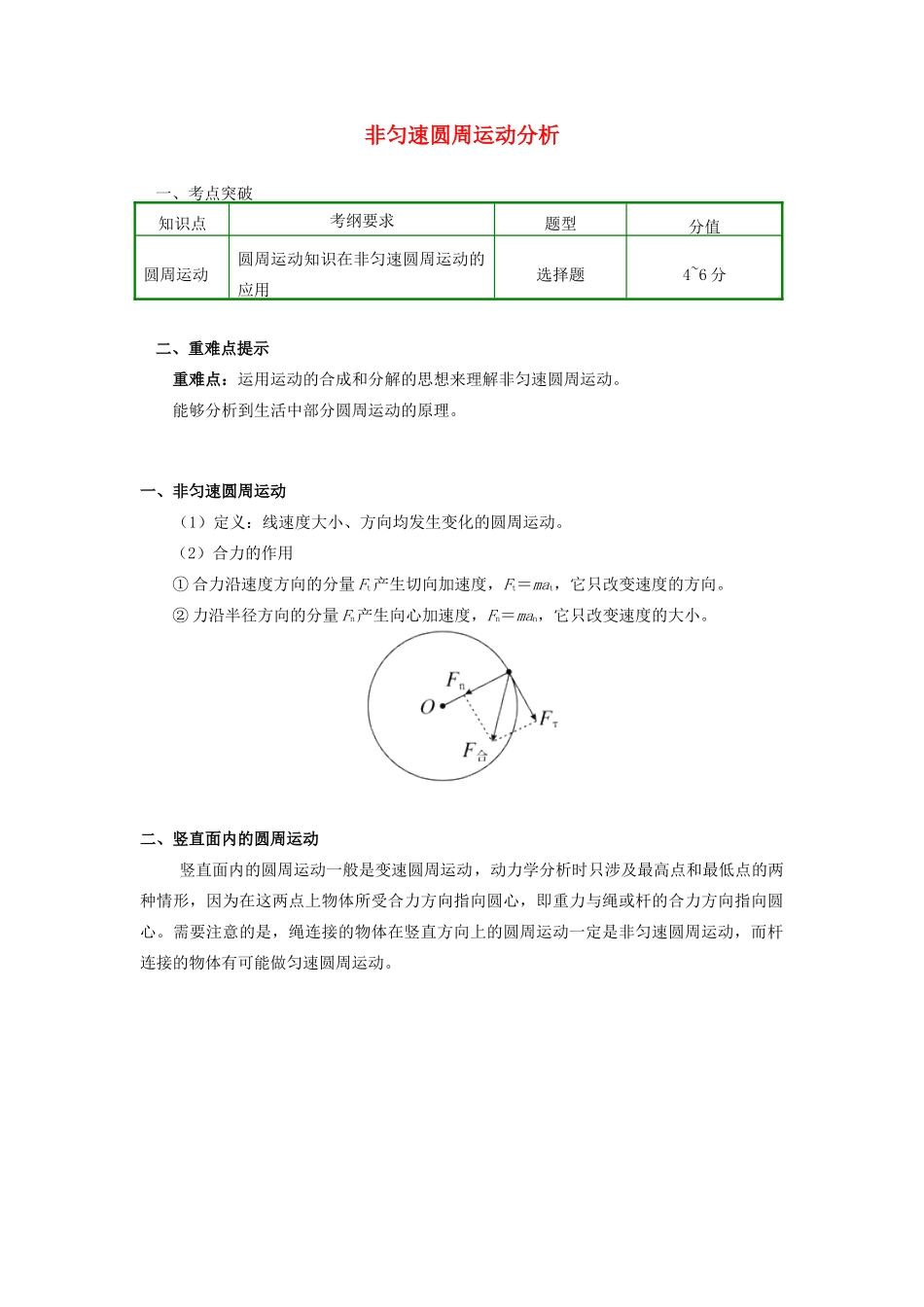
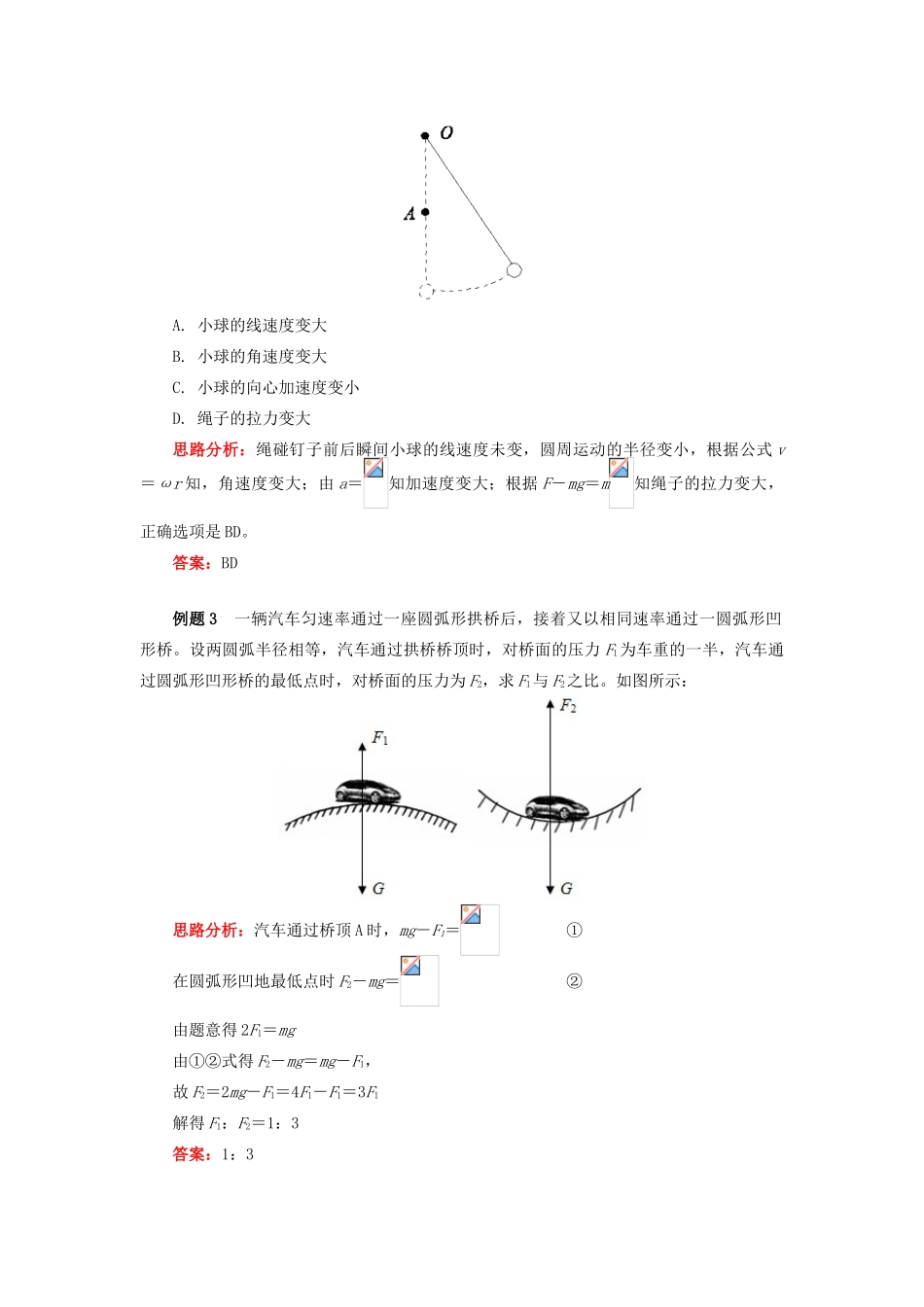
非匀速圆周运动分析一、考点突破知识点考纲要求题型分值圆周运动圆周运动知识在非匀速圆周运动的应用选择题4~6 分二、重难点提示重难点:运用运动的合成和分解的思想来理解非匀速圆周运动。能够分析到生活中部分圆周运动的原理。一、非匀速圆周运动(1)定义:线速度大小、方向均发生变化的圆周运动。(2)合力的作用① 合力沿速度方向的分量 Ft产生切向加速度,Ft=mat,它只改变速度的方向。② 力沿半径方向的分量 Fn产生向心加速度,Fn=man,它只改变速度的大小。二、竖直面内的圆周运动竖直面内的圆周运动一般是变速圆周运动,动力学分析时只涉及最高点和最低点的两种情形,因为在这两点上物体所受合力方向指向圆心,即重力与绳或杆的合力方向指向圆心。需要注意的是,绳连接的物体在竖直方向上的圆周运动一定是非匀速圆周运动,而杆连接的物体有可能做匀速圆周运动。 注意:竖直面内的圆周运动问题,涉及知识面比较广,既有临界问题,又有能量守恒的问题,后面会详细讨论。例题 1 如图,光滑的水平面上固定着一个半径在逐渐减小的螺旋形光滑水平轨道.一个小球以一定速度沿轨道切线方向进入轨道,下列物理量中数值将减小的是( )A. 周期 B. 线速度 C. 角速度 D. 向心加速度思路分析:轨道对小球的支持力与速度方向垂直,即加速度方向始终与线速度方向垂直,只改变其方向而不改变大小,故小球的线速度大小不变;故 B 错误;根据 v=ωr,线速度大小不变,转动半径减小,故角速度变大,C 错误;根据,角速度增加,故周期减小,A 正确;根据,转动半径减小,故向心加速度增加,D 错误。答案:A例题 2 如图所示,绳的一端悬于 O 点,另一端系一小球;在 O 点正下方 A 处有一钉子。现使小球由高处摆下,当绳摆到竖直位置时与钉子相碰,则绳碰钉子前与碰钉子后瞬间相比(不计空气阻力)( )A. 小球的线速度变大B. 小球的角速度变大C. 小球的向心加速度变小D. 绳子的拉力变大思路分析:绳碰钉子前后瞬间小球的线速度未变,圆周运动的半径变小,根据公式 v=ωr 知,角速度变大;由 a=知加速度变大;根据 F-mg=m知绳子的拉力变大,正确选项是 BD。答案:BD例题 3 一辆汽车匀速率通过一座圆弧形拱桥后,接着又以相同速率通过一圆弧形凹形桥。设两圆弧半径相等,汽车通过拱桥桥顶时,对桥面的压力 F1为车重的一半,汽车通过圆弧形凹形桥的最低点时,对桥面的压力为 F2,求 F1与 F2之比。如图所示:...