2014届高中数学 函数的单调性教案 北师大版必修1

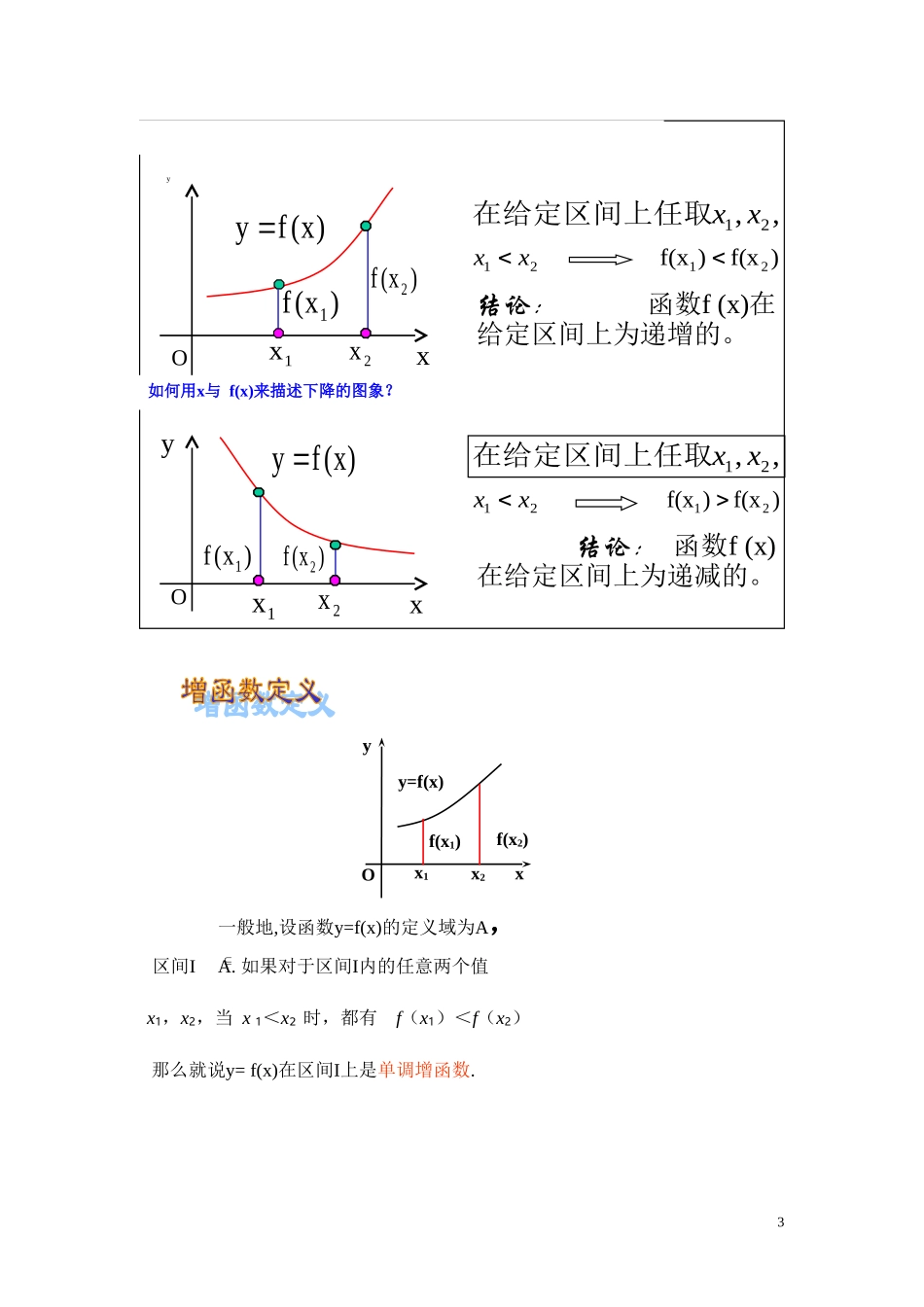
§3 函数的单调性教学目的：（1）通过已学过的函数特别是二次函数，理解函数的单调性及其几何意义；（2）学会运用函数图象理解和研究函数的性质；（3）能够熟练应用定义判断数在某区间上的的单调性．教学重点：函数的单调性及其几何意义．教学难点：利用函数的单调性定义判断、证明函数的单调性． 教学过程：阅读与思考1、阅读教材  P36 的实例分析及思考交流止。2、思考问题 （1）从 P36 图 2-15 （全国从 20120421-20120519 每日新增艾滋病例的变化统计图）看出，形势从何日开始好转？ （2）从 P36 图 2-16 你能否说出 y 随 x 如何变化？德国著名心理学家艾宾浩斯研究数据 时间间隔记忆保持量刚刚记忆完毕100%20 分钟之后58.2%1 小时之后44.2%8-9 小时之后35.8%1 天后33.7%2 天后27.8%6 天后25.4%一个月后21.1% … …艾宾浩斯遗忘曲线1问:什么是增函数、减函数、函数的单调性？问题 1、 作出下列函数的图象,并指出图象的变化趋势:问题 2、你能明确地说出“图象呈逐渐上升或下降趋势”的意思吗？在某一区间内，图象在该区间呈上升趋势 当 x 的值增大时，函数值 y 也增大图象在该区间呈下降趋势 当 x 的值增大时，函数值 y 反而减小如何用 x 与 f(x)来描述上升的图象？保持量（百分数）天数1 2 3 4 5 6020406080100Oxy2x2y21yOxx1y Oxy1xy1-1yOx2xy2,,21 xx在给定区间上任取21xx )f(x)f(x21 结论： 函数f (x)在给定区间上为递增的。Oxy)x(fy )x(f11x如何用x与 f(x)来描述下降的图象？,,21 xx在给定区间上任取21xx  结论： 函数f (x)在给定区间上为递减的。)f(x)f(x21 )x(f1)x(f2)x(fy Oxy1x2x)x(f22xxyOy=f(x)x1x2f(x1)f(x2)那么就说y= f(x)在区间I上是单调增函数.一般地,设函数y=f(x)的定义域为A， 区间I A. 如果对于区间I内的任意两个值x1，x2，当 x 1＜x2 时，都有 f（x1）＜f（x2）3单调区间如果函数 y=f(x)在区间 I 是单调增函数或单调减函数,那么就说函数 y=f(x)在区间 I 上具有单调性. 单调增区间和单调减区间统称为单调区间.xyOy=f(x)x1x2f(x1)f(x2)那么就说y= f(x)在区间I上是单调增函数.一般地,设函数y=f(x)的定义域为A， 区间I A. 如果对于区间I内的任意两个值x1，x2，当 x 1＜x2 时，都有 f（x1）＜f（x2））上是增函数。，（在区间证明函数 xxf12)( [例1]内任意是区间设),(,x 21...