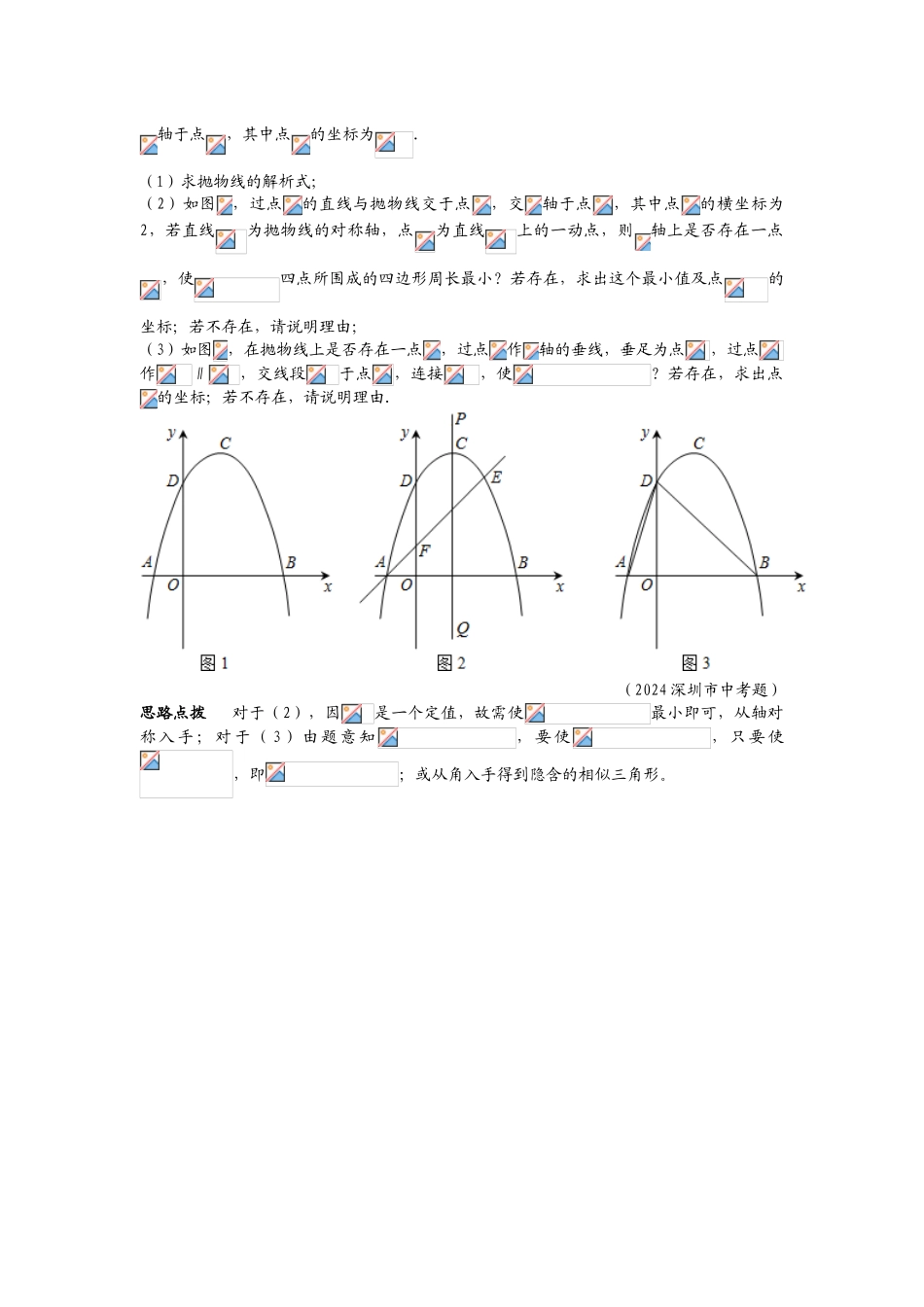
抛物线与直线形(1) ——由动点生成的特别三角形问题知识点归纳抛物线与直线形的结合表现形式之一是,以抛物线为载体,探讨是否存在一些点,使其能够成某些特别三角形,有以下常见的基本形式:(1)抛物线上的点能否构成等腰三角形;(2)抛物线上的点能否构成直角三角形;(3)抛物线上的点能否构成相似三角形;解这类问题的基本思路:假设存在,数形结合,分类归纳,逐一考察。经典例题【例 1】如图,抛物线经过的三个顶点,已知∥轴,点在轴上,点在轴上,且. (1)求抛物线的对称轴;(2)写出三点的坐标并求抛物线的解析式;(3)探究:若点是抛物线对称轴上且在轴下方的动点,是否存在是等腰三角形?若存在,求出所有符合条件的点坐标;不存在,请说明理由.(龙岩市中考题)思路点拨 对于(3)只需求出点纵坐标,将问题转化为相关线段长。解题的关键是分情况讨论并正确画图。【例 2】已知抛物线,交轴于两点(在的左边),交轴于点,且有最大值.(1)求抛物线的解析式;(2)在抛物线上是否存在点,使是直角三角形?若存在,求出点坐标;若不存在,说明理由.(包头市中考题)思路点拨 对于(2),设点坐标为,寻找相似三角形,建立的另一关系式,解联立而得到的方程组,可求出的值。【例 3】抛物线与轴交于点,顶点为,对称轴与轴交于点.(1)如图 .求点的坐标及线段 OC 的长;(2)点在抛物线上,直线∥交轴于点,连接.① 若含角的直角三角板如图所示放置.其中,一个顶点与点重合,直角顶点在上,另一个顶点 E 在上.求直线的函数解析式;② 若含角的直角三角板一个顶点与点重合,直角顶点在直线上,另一个顶点在上,求点的坐标.(2024 年绍兴市中考题)思路点拨 对于(2),解题的关键是求出的长。由条件出发,构造全等三角形或相似三角形,而能发现四点共圆,可使问题获得简解。【例 4】如图 ,抛物线的顶点为,交轴于两点,交轴于点,其中点的坐标为.(1)求抛物线的解析式;(2)如图,过点的直线与抛物线交于点,交轴于点,其中点的横坐标为2,若直线为抛物线的对称轴,点为直线上的一动点,则轴上是否存在一点,使四点所围成的四边形周长最小?若存在,求出这个最小值及点的坐标;若不存在,请说明理由;(3)如图,在抛物线上是否存在一点,过点作轴的垂线,垂足为点,过点作∥,交线段于点,连接,使?若存在,求出点的坐标;若不存在,请说明理由.(2024 深圳市中考题)思路点拨 对于(2),因是...