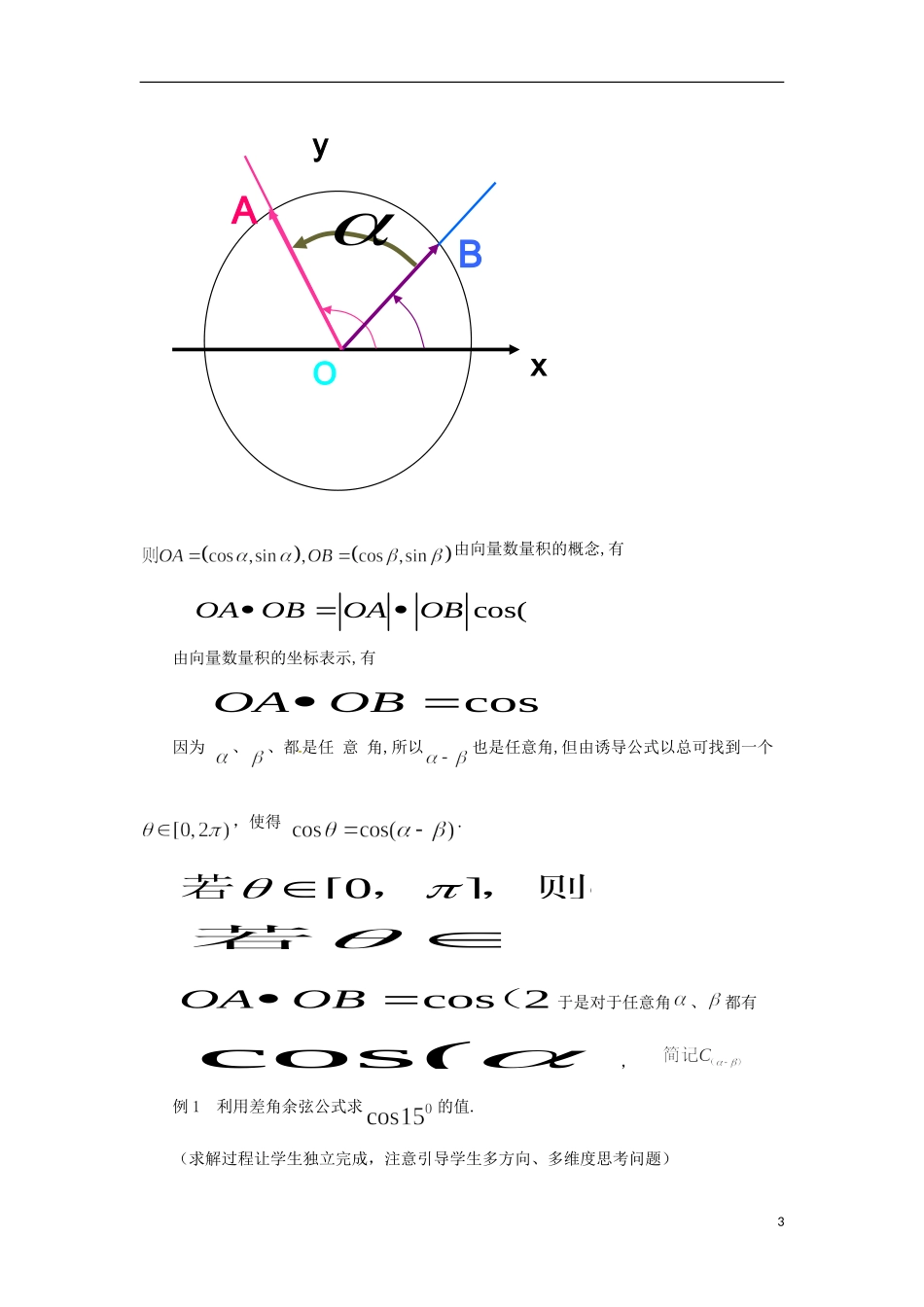
3.1.《两角和与差的正弦、余弦和正切公式》导学案【学习目标】1.掌握两角和与差公式的推导过程;2.培养学生利用公式求值、化简的分析、转化、推理能力;3.发展学生的正、逆向思维能力,构建良好的思维品质;4.引导学生建立两角差的余弦公式.通过公式的简单应用,使学生初步理解公式的结构及其功能,并为建立其他和差公式打好基础.【导入新课】创设情景,揭示课题以学校教学楼为背景素材(见课件)引入问题.并针对问题中的用计算器或不用计算器计算求值,以激趣激疑,导入课题.教师问:想一想: 学校因某次活动的需要,需从楼顶的 C 点处往该点正对的地面上的 A点处拉一条钢绳,为了在购买钢绳时不至于浪费,你能算一算到底需要多长钢绳吗? (要求在地面上测量,测量工具:皮尺,测角器)问题:(1)能不能不用计算器求值 : , ,?(2)设计意图:由给出的背景素材,使学生感受数学源于生活,又应用于生活,唤起学生解决问题的兴趣,和抛出新知识引起学生的疑惑,在兴趣和疑惑中,激发学生的求知欲,引导学习方向.新授课阶段一、两角差的余弦公式的推导过程1.三角函数线法:问:①怎样作出角、、的终边?②怎样作出角的余弦线 OM?③怎样利用几何直观寻找 OM 的表示式?设计意图:尽量用动画课件把探索过程展示出来,使学生能从几何直观角度加强对公式结构形式的认识.1α-ββαp1CBAMPOXY(1) 设角终边与单位圆地交点为 P1,.(2) 过点 P 作 PM⊥X 轴于点 M,那么 OM 就是 的余弦线.(3) 过点 P 作 PA⊥OP1 于 A,过点 A 作 AB⊥x 轴于 B,过点 P作 PC⊥AB 于 C那么 OA 表示 ,AP 表示,并且于是 OM=OB+BM=OB+CP=OA+AP=最后要提醒注意,公式推导的前提条件:、、都是锐角,且.2.向量法:问:①结合图形,明确应选哪几个向量,它们怎么表示?② 怎样利用向量数量积的概念和计算公式得到结果?③ 对探索的过程进一步严谨性的思考和处理,从而得到合理的科学结论.设计意图:让学生经历利用向量知识解决一个数学问题的过程,体会向量方法解决数学问题的简洁性.2如图,建立单位圆O 由向量数量积的概念,有cos()cos()OAOBOAOB� 由向量数量积的坐标表示,有coscossinsin.OAOB� 因为 、、都是任 意 角,所以也是任意角,但由诱导公式以总可找到一个,使得 .[0]coscosOAOB�若,,则();[2[0若,2),则,),且cos 2coscosOAOB...