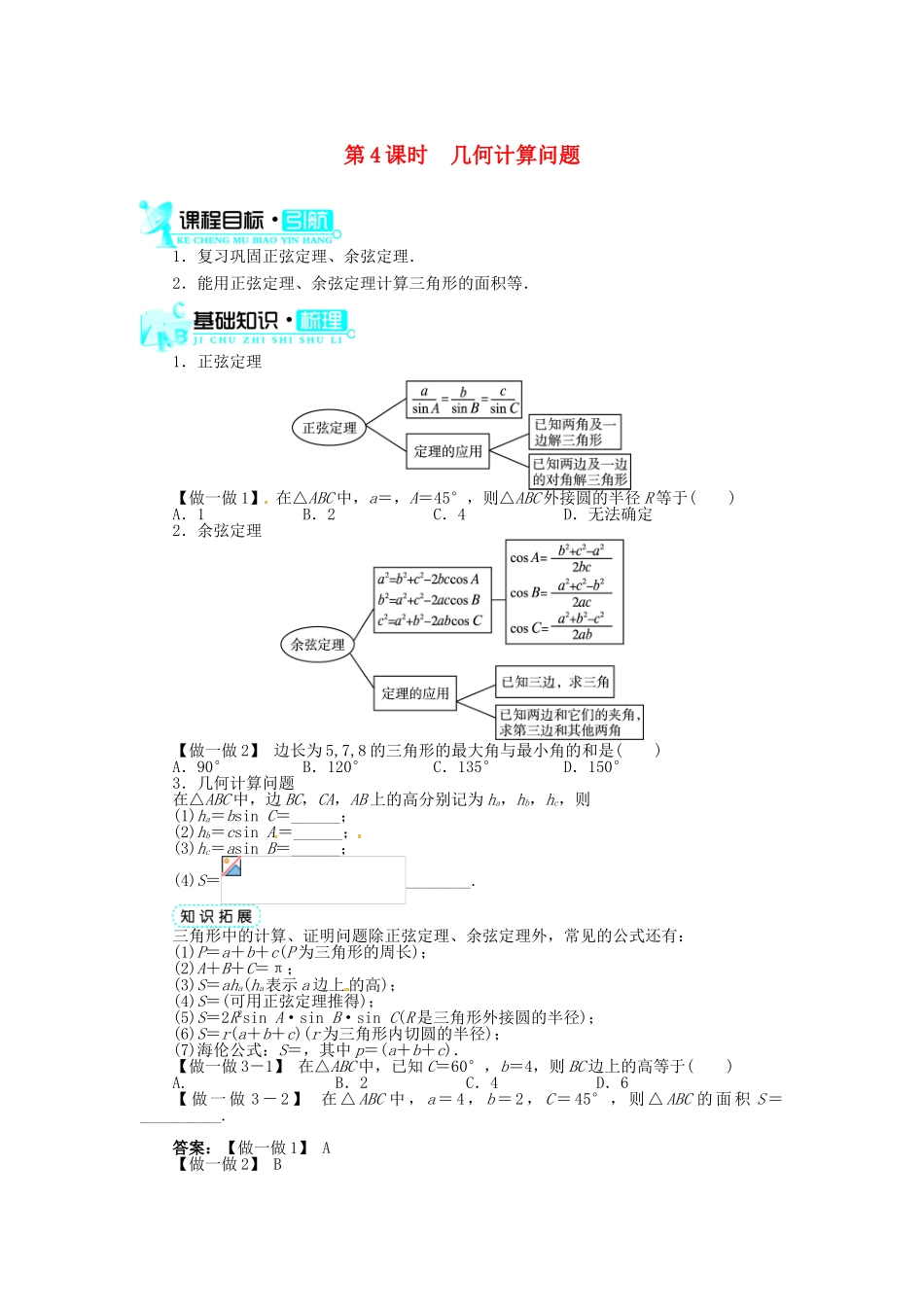
第 4 课时 几何计算问题1.复习巩固正弦定理、余弦定理.2.能用正弦定理、余弦定理计算三角形的面积等.1.正弦定理【做一做 1】 在△ABC 中,a=,A=45°,则△ABC 外接圆的半径 R 等于( )A.1 B.2C.4 D.无法确定2.余弦定理【做一做 2】 边长为 5,7,8 的三角形的最大角与最小角的和是( )A.90° B.120° C.135° D.150°3.几何计算问题在△ABC 中,边 BC,CA,AB 上的高分别记为 ha,hb,hc,则(1)ha=bsin C=______;(2)hb=csin A=______;(3)hc=asin B=______;(4)S=________.三角形中的计算、证明问题除正弦定理、余弦定理外,常见的公式还有:(1)P=a+b+c(P 为三角形的周长);(2)A+B+C=π;(3)S=aha(ha表示 a 边上 的高);(4)S=(可用正弦定理推得);(5)S=2R2sin A·sin B·sin C(R 是三角形外接圆的半径);(6)S=r(a+b+c)(r 为三角形内切圆的半径);(7)海伦公式:S=,其中 p=(a+b+c).【做一做 3-1】 在△ABC 中,已知 C=60°,b=4,则 BC 边上的高等于( )A. B.2 C.4 D.6【 做 一 做 3 - 2 】 在 △ ABC 中 , a = 4 , b = 2 , C = 45° , 则 △ ABC 的 面 积 S =__________.答案:【做一做 1】 A【做一做 2】 B3.(1)csin B (2)asin C (3)bsin A (4)bcsin A【做一做 3-1】 D【做一做 3-2】 21.三角形中的常用结论剖析:在△ABC 中,边、角之间的关系有以下常用结论:①a+b>c,b+c>a,c+a>b.②a-b<c,b-c<a,a-c<b.③A+B+C=π.④a>bA>Bsin A>sin B.⑤a=bA=B.⑥A 为锐角cos A>0a2<b2+c2;A 为钝角cos A<0a2>b2+c2;A 为直角cos A=0a2=b2+c2.⑦sin(A+B)=sin C,cos(A+B)=-cos C.⑧sin =cos ,cos =sin .2.解三角形剖析:解三角形有四种情况,如下表所示:已知条件应用定理一般解法一边和两角(如a,B,C)正弦定理由 A+B+C=180°,求角 A;由正弦定理求出 b 与c;S△ABC=acsin B;在有解时只有一解两边和夹角(如a,b,C)余弦定理正弦定理由余弦定理求第三边 c;由正弦定理求出小边所对的角;再由 A+B+C=180°求出另一角;S△ABC=absin C;在有解时只有一解三边(a,b,c)余弦定理由余弦定理求出角 A,B;再利用 A+B+C=180°,求出角 C;S△ABC=absin C;在有解时只有一解两边和其中一边的对角(如 a,b,A)正弦定理...