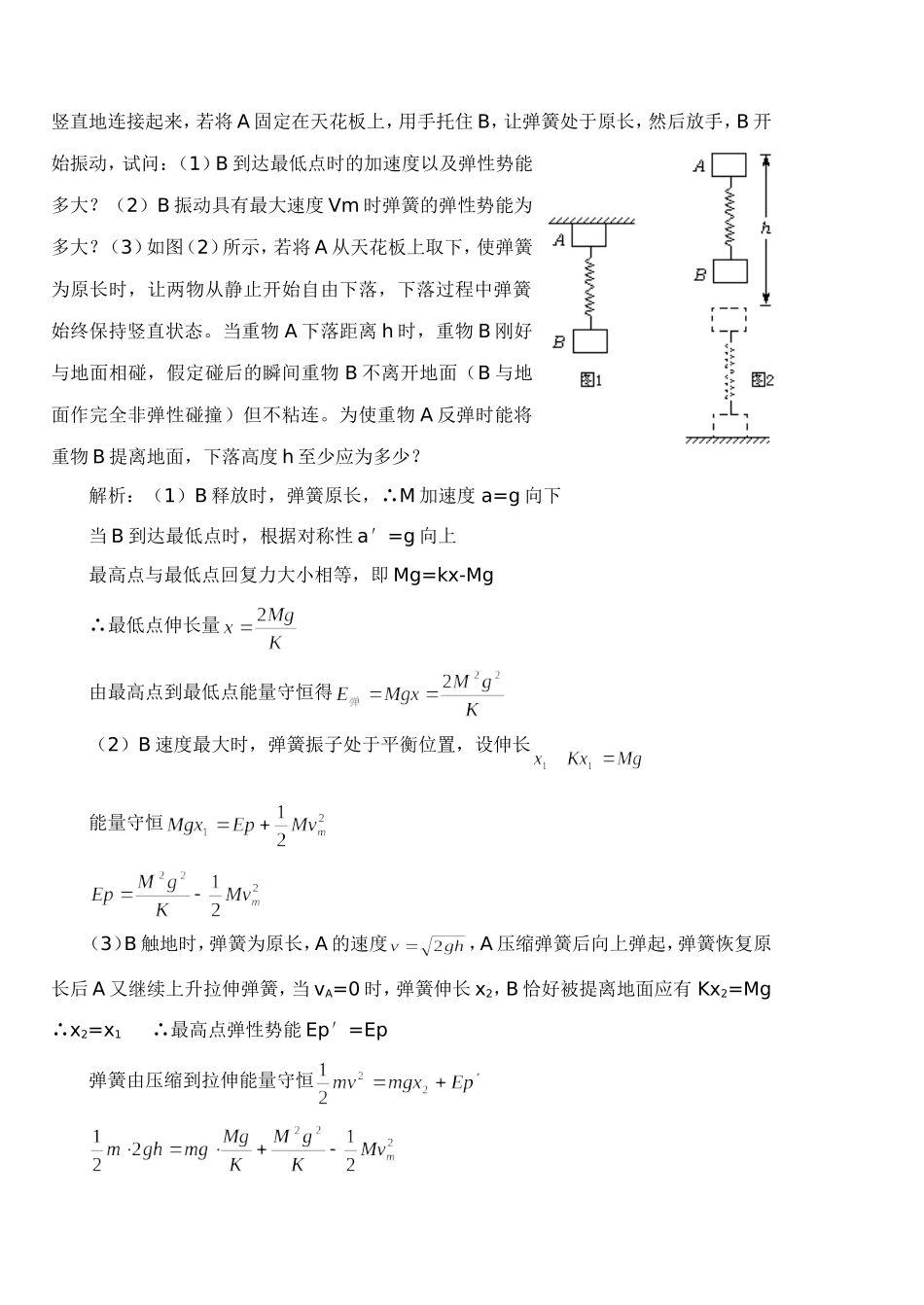
巧用弹簧振子简谐振动过程的对称性解题江苏省泰兴中学 李小东(邮编 225400)对称性是简谐运动的重要性质之一,在关于平衡位置对称点上位移,回复力,加速度,速度,动能,势能数值均相等,振动物体沿不同方向经过同一路径或通过关于平衡位置两段对称路程的时间相等,利用对称规律解题,往往事半功倍,下面以弹簧振子为例加以说明:一、时间、速度的对称性例 1、如图,在水平方向做简谐运动的弹簧振子,质量为 m,A、B 两点关于平衡位置对称,经过 A 点时速度为 v。(1)它从平衡位置 O 点经过 0.4s 第一次到达 A 点,再经过 0.2s 第二次到达 A点,从弹簧振子离开 O 点开始计时,则振子第三次到达 A 点时间是多少?(2)振子连续经过 A、B 两点,弹力所做的功以及弹力的冲量是多少?解析:(1)①若开始经过 O 点速度方向向右由时间对称性:∴② 若开始经过 O 点的运动方向向左T=2S(2)由速度的对称性知连续经过 A、B 两点 vA与 vB大小相等,但方向可能相同或相反。∴W 弹=△Ek=0,I 弹=0 或 I 弹=2mv二、加速度、回复力的对称性例 2、如图(1)所示,质量分别为 m 和 M 的 A、B 两重物用劲度系数为 k 的轻质弹簧竖直地连接起来,若将 A 固定在天花板上,用手托住 B,让弹簧处于原长,然后放手,B 开始振动,试问:(1)B 到达最低点时的加速度以及弹性势能多大?(2)B 振动具有最大速度 Vm 时弹簧的弹性势能为多大?(3)如图(2)所示,若将 A 从天花板上取下,使弹簧为原长时,让两物从静止开始自由下落,下落过程中弹簧始终保持竖直状态。当重物 A 下落距离 h 时,重物 B 刚好与地面相碰,假定碰后的瞬间重物 B 不离开地面(B 与地面作完全非弹性碰撞)但不粘连。为使重物 A 反弹时能将重物 B 提离地面,下落高度 h 至少应为多少?解析:(1)B 释放时,弹簧原长,∴M 加速度 a=g 向下当 B 到达最低点时,根据对称性 a′=g 向上最高点与最低点回复力大小相等,即 Mg=kx-Mg ∴最低点伸长量由最高点到最低点能量守恒得(2)B 速度最大时,弹簧振子处于平衡位置,设伸长能量守恒 (3)B 触地时,弹簧为原长,A 的速度,A 压缩弹簧后向上弹起,弹簧恢复原长后 A 又继续上升拉伸弹簧,当 vA=0 时,弹簧伸长 x2,B 恰好被提离地面应有 Kx2=Mg ∴x2=x1 ∴最高点弹性势能 Ep′=Ep弹簧由压缩到拉伸能量守恒三、弹簧振子关于平衡位置对称的两点位移...