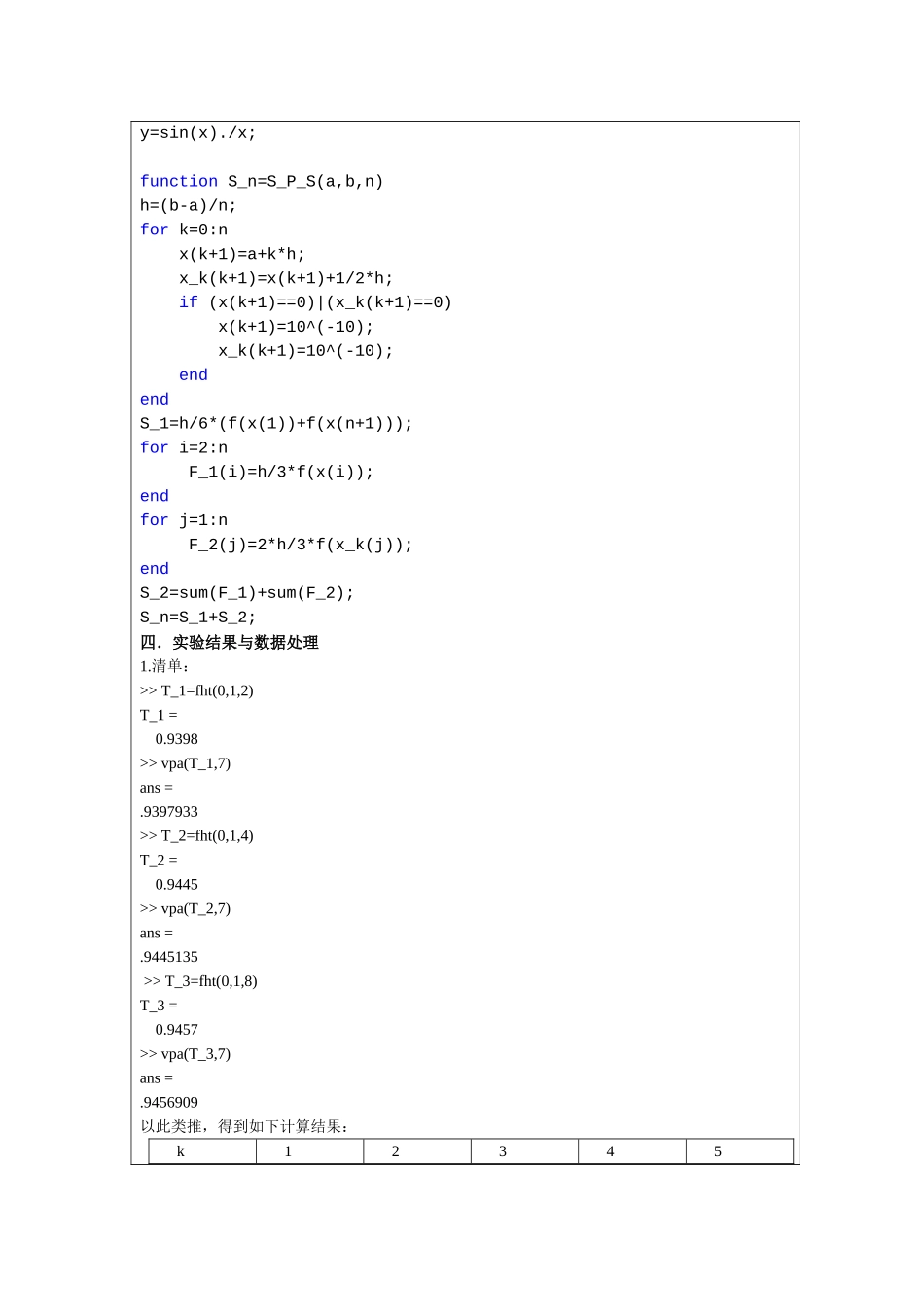
宁夏师范学院数学与计算机科学学院《数值分析》实验报告实验序号:4 实验项目名称:复合梯形公式、复合辛普森公式学 号姓 名专业、班级实验地点指导老师时 间2025 年 11 月 6 日一、实验目的及要求 1.掌握复合梯形公式与复合辛普森公式的基本思想。 2.编程实现用复合梯形公式与复合辛普森公式求积分。 3.熟悉 matlab 软件的使用。二、实验设备(环境)及要求1、环境要求:硬件:一般要求 486 以上的处理器、16MB 以上内存、足够的的硬盘可用空间 (随安装组件的多少而定);软件:MATLAB 编程软件。三、实验内容及步骤计算积分值:I=.1.复合梯形公式:源程序:function y=fx(x) y=sin(x)./x;function T_n=fht(a,b,n) h=(b-a)/n; for k=0:n x(k+1)=a+k*h; if x(k+1)==0 x(k+1)=10^(-10); endendT_1=h/2*(fx(x(1))+fx(x(n+1))); for i=2:n F(i)=h*fx(x(i)); endT_2=sum(F); T_n=T_1+T_2;2.复合辛普森公式:源程序:function y=f(x) y=sin(x)./x;function S_n=S_P_S(a,b,n) h=(b-a)/n;for k=0:n x(k+1)=a+k*h; x_k(k+1)=x(k+1)+1/2*h; if (x(k+1)==0)|(x_k(k+1)==0) x(k+1)=10^(-10); x_k(k+1)=10^(-10); endendS_1=h/6*(f(x(1))+f(x(n+1)));for i=2:n F_1(i)=h/3*f(x(i)); endfor j=1:n F_2(j)=2*h/3*f(x_k(j)); endS_2=sum(F_1)+sum(F_2); S_n=S_1+S_2;四.实验结果与数据处理1.清单:>> T_1=fht(0,1,2)T_1 = 0.9398>> vpa(T_1,7)ans = .9397933>> T_2=fht(0,1,4)T_2 = 0.9445>> vpa(T_2,7)ans =.9445135 >> T_3=fht(0,1,8)T_3 = 0.9457>> vpa(T_3,7)ans =.9456909以此类推,得到如下计算结果: k 1 2 3 4 5 Tn 0.9397933 0.9445135 0.9456909 0.9459850 0.9460596 k 6 7 8 9 10 Tn 0.9460769 0.9460815 0.9460827 0.9460830 0.94603812.清单:>> S_1=S_P_S(0,1,2)S_1 = 0.9495>> vpa(S_1,7) ans = .9495483 >> S_2=S_P_S(0,1,4)S_2 = 0.9465>> vpa(S_2,7)ans = .9465170 >> S_3=S_P_S(0,1,8)S_3 = 0.9461>> vpa(S_3,7)ans = .9461373 >> S_4=S_P_S(0,1,16)S_4 = 0.9461>> vpa(S_4,7) ans =.9460899 >> S_5=S_P_S(0,1,32)S_5 = 0.9461>> vpa(S_5,7) ans =.9460839 五、分析与讨论简单的分析我们认为通过对 h 的值的改变,只要 h 值越小,即等分的区间越小,结果应该更加精确,精确度越高。经过实验的验证,也表明我们的推理正确,无论是复合梯形公式还是复合辛普森公式它们最终结果都会随着 h 值的减小而更加精确。复合梯形公式和复合辛普森公式计算出的结果进行比较,发现复合辛普森公式计算出的结果更加的精确。六、老师评语签名: 日期: 年 月 日 成绩