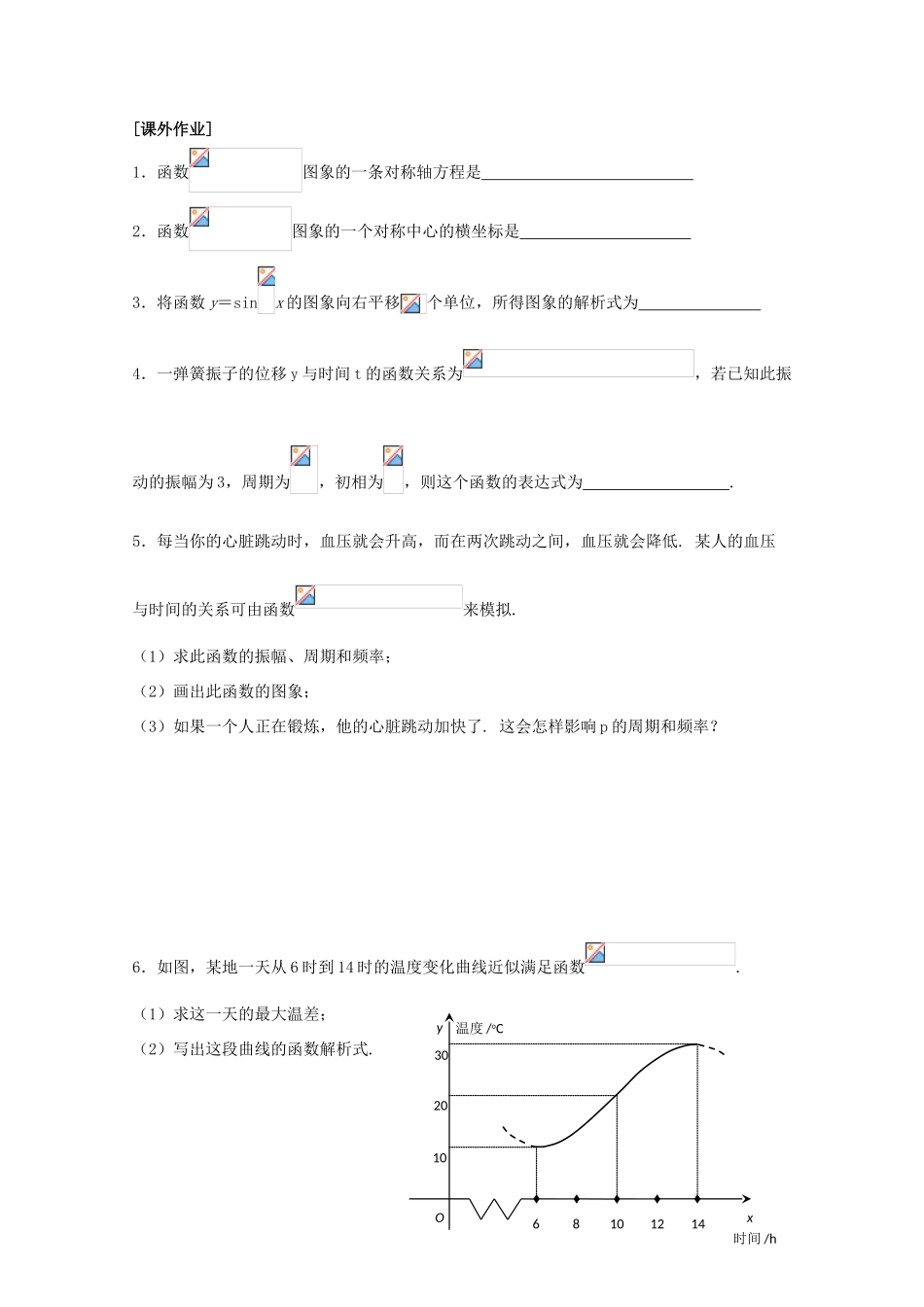
[课 题]:1.3.4 三角函数的应用(一)[知识摘记][例题解析]例 1.如图所示,点 O 为做简谐运动的物体的平衡位置,取向右的方向为物体位移的正方向,若已知振幅为 3cm,周期为 3s,且物体向右运动到平衡位置最远处时开始计时.(1)求物体对平衡位置的位移 x(cm)和时间 t(s)之间的函数关系;(2)求该物体在 t=5s 时的位置. 例 2.一半径为 3m 的水轮如图所示,水轮圆心 O 距离水面 2m,已知水轮每分钟转动 4 圈,如果当水轮上点 P 从水中浮现时(图中点 P0)开始计算时间.(1)将点 P 距离水面的高度 z(m)表示为时间 t(s)的函数; (2)点 P 第一次到达最高点大约需要多长时间?例 3.如图所示,一个摩天轮半径为 10m,轮子的底部在地面上 2 米处,如果此摩天轮每 20s 转一圈,且当摩天轮上某人经过点 P 处(点 P 与摩天轮中心高度相同)时开始计时.(1)求此人相对于地面的高度关于时间的关系式;(2)在摩天轮转动的一圈内,约有多长时间此人相对于地面的高度不超过 10m.小结:应用三角函数模型解决实际问题,一般步骤:[练习与反思] 课本练习反思:Oxy68101214201030温度 /oC时间 /h[课外作业] 1.函数图象的一条对称轴方程是 2.函数图象的一个对称中心的横坐标是 3.将函数 y=sinx 的图象向右平移个单位,所得图象的解析式为 4.一弹簧振子的位移 y 与时间 t 的函数关系为,若已知此振动的振幅为 3,周期为,初相为,则这个函数的表达式为 .5.每当你的心脏跳动时,血压就会升高,而在两次跳动之间,血压就会降低. 某人的血压与时间的关系可由函数来模拟.(1)求此函数的振幅、周期和频率;(2)画出此函数的图象;(3)如果一个人正在锻炼,他的心脏跳动加快了. 这会怎样影响 p 的周期和频率?6.如图,某地一天从 6 时到 14 时的温度变化曲线近似满足函数.(1)求这一天的最大温差;(2)写出这段曲线的函数解析式.