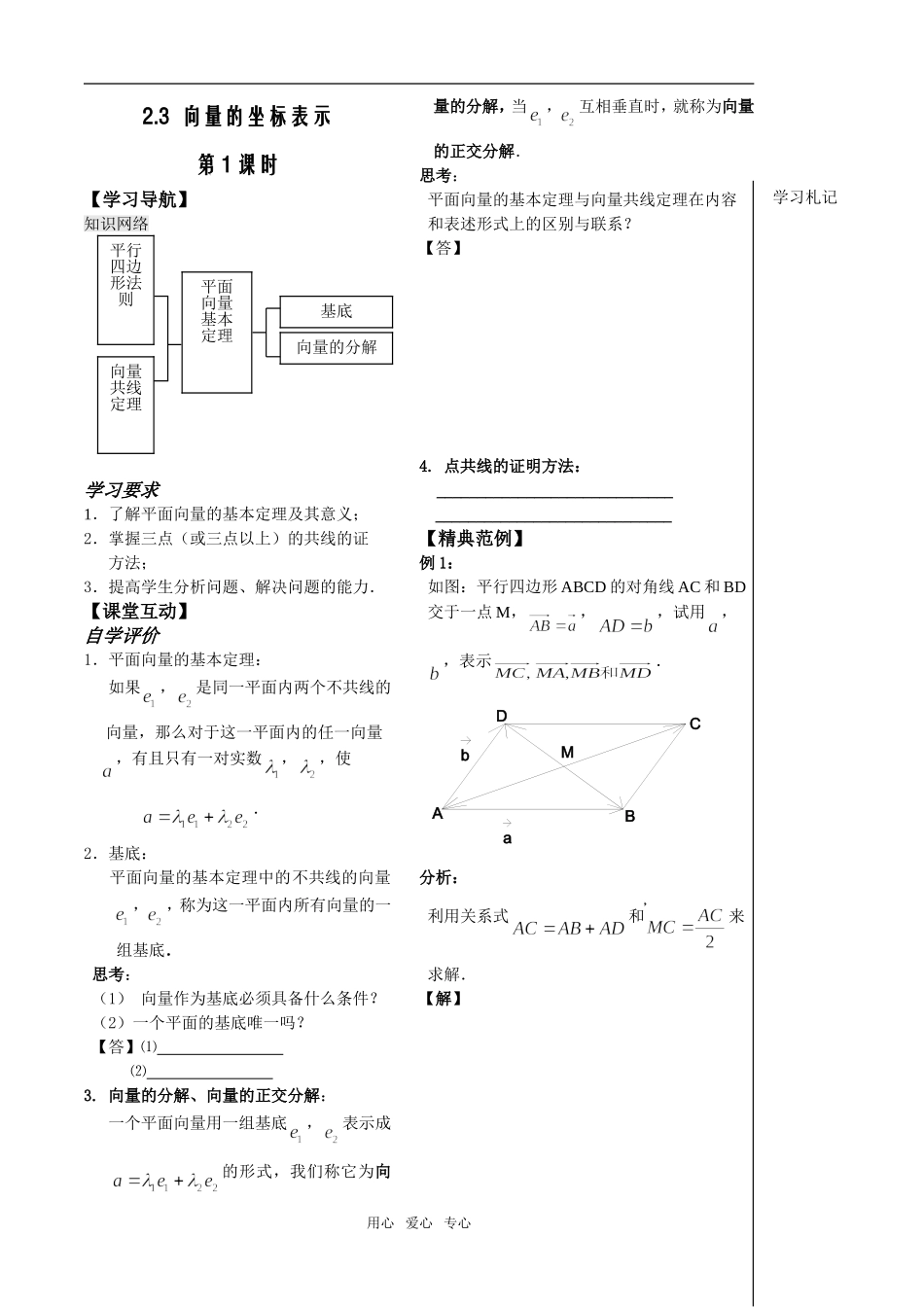
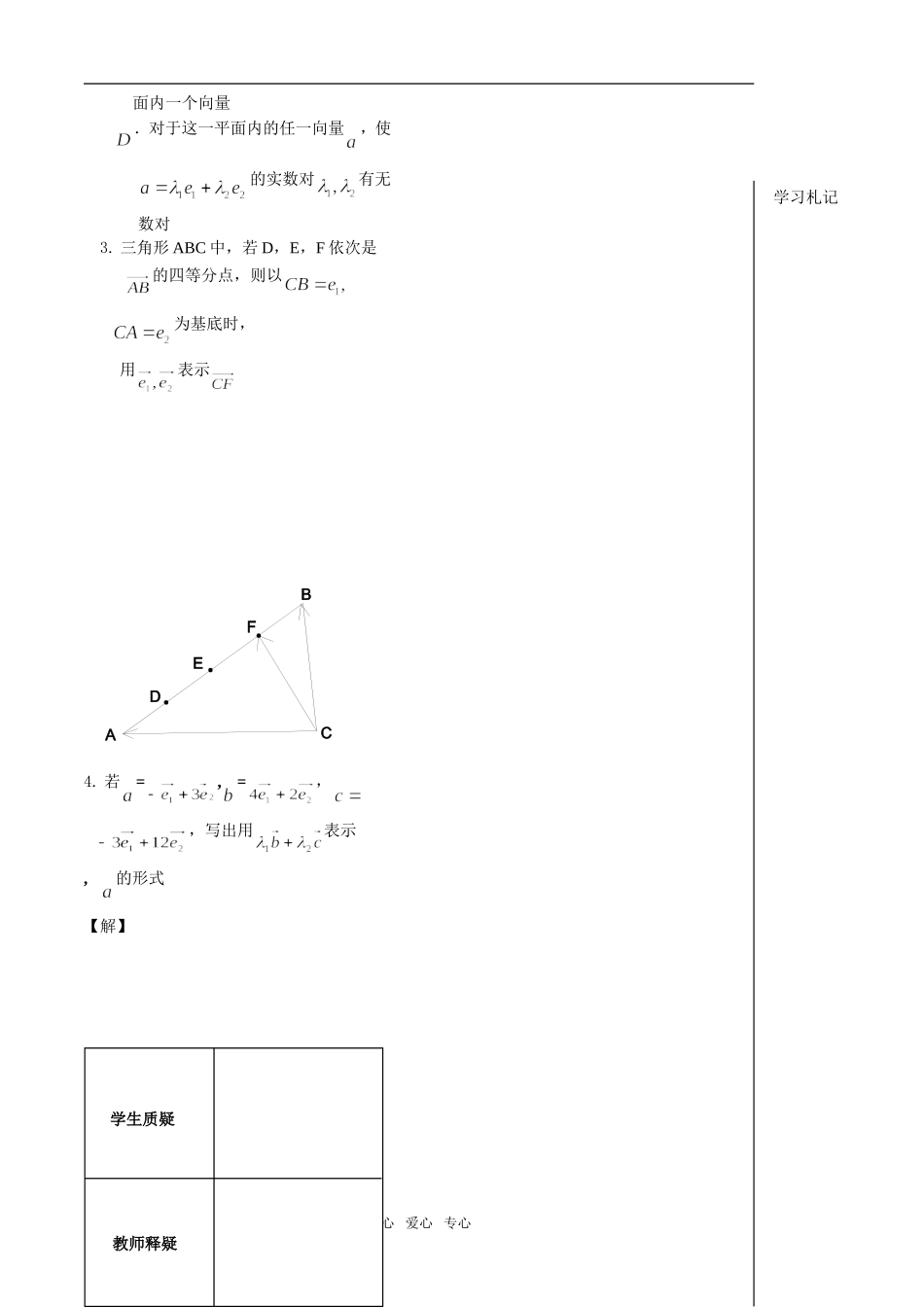
2.3 向量的坐标表示第 1 课时 【学习导航】 知识网络 学习要求 1.了解平面向量的基本定理及其意义;2.掌握三点(或三点以上)的共线的证方法;3.提高学生分析问题、解决问题的能力.【课堂互动】自学评价1.平面向量的基本定理: 如果,是同一平面内两个不共线的向量,那么对于这一平面内的任一向量,有且只有一对实数,,使 .2.基底: 平面向量的基本定理中的不共线的向量,,称为这一平面内所有向量的一 组基底.思考:(1) 向量作为基底必须具备什么条件?(2)一个平面的基底唯一吗?【答】⑴ ⑵ 3. 向量的分解、向量的正交分解: 一个平面向量用一组基底,表示成 的形式,我们称它为向量的分解,当,互相垂直时,就称为向量的正交分解.思考:平面向量的基本定理与向量共线定理在内容和表述形式上的区别与联系?【答】4. 点共线的证明方法: _____________________________ _____________________________【精典范例】例 1: 如图:平行四边形 ABCD 的对角线 AC 和 BD 交于一点 M,,,试用, ,表示.baMDBCA分析: 利用关系式和来 求解.【解】用心 爱心 专心向量共线定理向量的分解基底平行四边形法则平面向量基本定理学习札记点评:(1)画图,直观,形象,具体化.(2)把所求向量放到三角形或平行四边形中, 运用法则进行求解.例 2:设是平面 的一组基底,如果 ,求证:A、B、D 三点共线.分析: 欲证 A、B、D 三点共线,只需证明共起点的两个向量与共线,即证 .【证明】点评: (1) 将点共线问题转化为向量共线问题; (2)共起点(或共终点)的必要性,点的选择任意.例 3: 如图,在平行四边形 ABCD 中,点在 AB的延长线上,且,点在上,且,用向量法证明: 、、 三点共线MNDCBA分析: 只需证明与共线,即等于某一个实数与的积,可选择一组 向量为基底,把、都用基底来 表示. 【证明】点评: 证明两个向量共线,可以选择一组恰当的 基底来表示这两个向量.追踪训练1.若是平面内所有向量的一组基底,则 下面的四组向量中不能作为一组基底的是 ( ) .和 .与 .和.与2. 若是平面内所有向量的一组基底, 那么下列结论成立的是 ( ).若实数使,则 .空间任意都可以表示为 ∈R .∈R 不一定表示平用心 爱心 专心学习札记面内一个向量.对于这一平面内的任一向量,使 的实数对有无 数对3. 三角形 ABC 中,若 D,E,F 依次是的四等分点,则以为基底时,用表示 FEDCBA4. 若=,=, ,写出用表示, 的形式【解】【师生互动】用心 爱心 专心学生质疑教师释疑学习札记