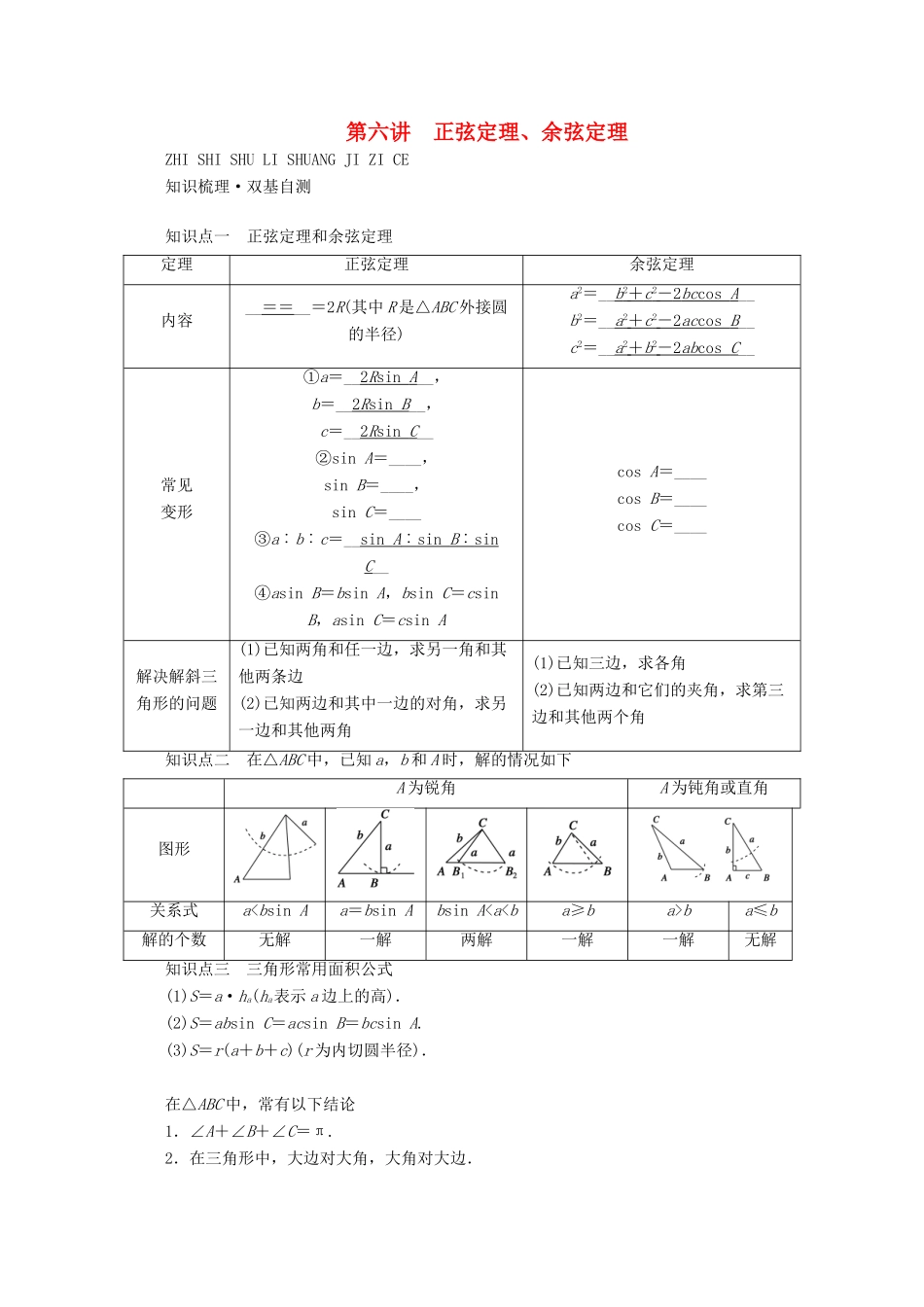
第六讲 正弦定理、余弦定理ZHI SHI SHU LI SHUANG JI ZI CE知识梳理·双基自测 知识点一 正弦定理和余弦定理定理正弦定理余弦定理内容__==__=2R(其中 R 是△ABC 外接圆的半径)a2=__b 2 + c 2 - 2 bc cos A __b2=__a 2 + c 2 - 2 ac cos B __c2=__a 2 + b 2 - 2 ab cos C __常见变形①a=__2 R sin A __,b=__2 R sin B __,c=__2 R sin C __②sin A=____,sin B=____,sin C=____③a︰b︰c=__sin A ︰ sin B ︰ sin C__④asin B=bsin A,bsin C=csin B,asin C=csin Acos A=____cos B=____cos C=____解决解斜三角形的问题(1)已知两角和任一边,求另一角和其他两条边(2)已知两边和其中一边的对角,求另一边和其他两角(1)已知三边,求各角(2)已知两边和它们的夹角,求第三边和其他两个角知识点二 在△ABC 中,已知 a,b 和 A 时,解的情况如下A 为锐角A 为钝角或直角图形关系式a
ba≤b解的个数无解一解两解一解一解无解知识点三 三角形常用面积公式(1)S=a·ha(ha表示 a 边上的高).(2)S=absin C=acsin B=bcsin A.(3)S=r(a+b+c)(r 为内切圆半径).在△ABC 中,常有以下结论1.∠A+∠B+∠C=π.2.在三角形中,大边对大角,大角对大边.3.任意两边之和大于第三边,任意两边之差小于第三边.4.sin (A+B)=sin C;cos (A+B)=-cos C;tan (A+B)=-tan C;sin =cos ,cos =sin .5.tan A+tan B+tan C=tan A·tan B·tan C.6.∠A>∠B⇔a>b⇔sin A>sin B⇔cos AB 必有 sin A>sin BB.在△ABC 中,角 A、B、C 所对的边分别为 a,b,c 且 a=1,c=,A=,则 b=1 或 2C.若满足条件 C=60°,AB=,BC=a 的△ABC 有两个,则实数 a 的取值范围是(,2)D.在△ABC 中,若 bcos B=acos A,则△ABC 是等腰三角形题组二 走进教材2.(必修 5P10A 组 T8 改编)△ABC 的内角 A,...