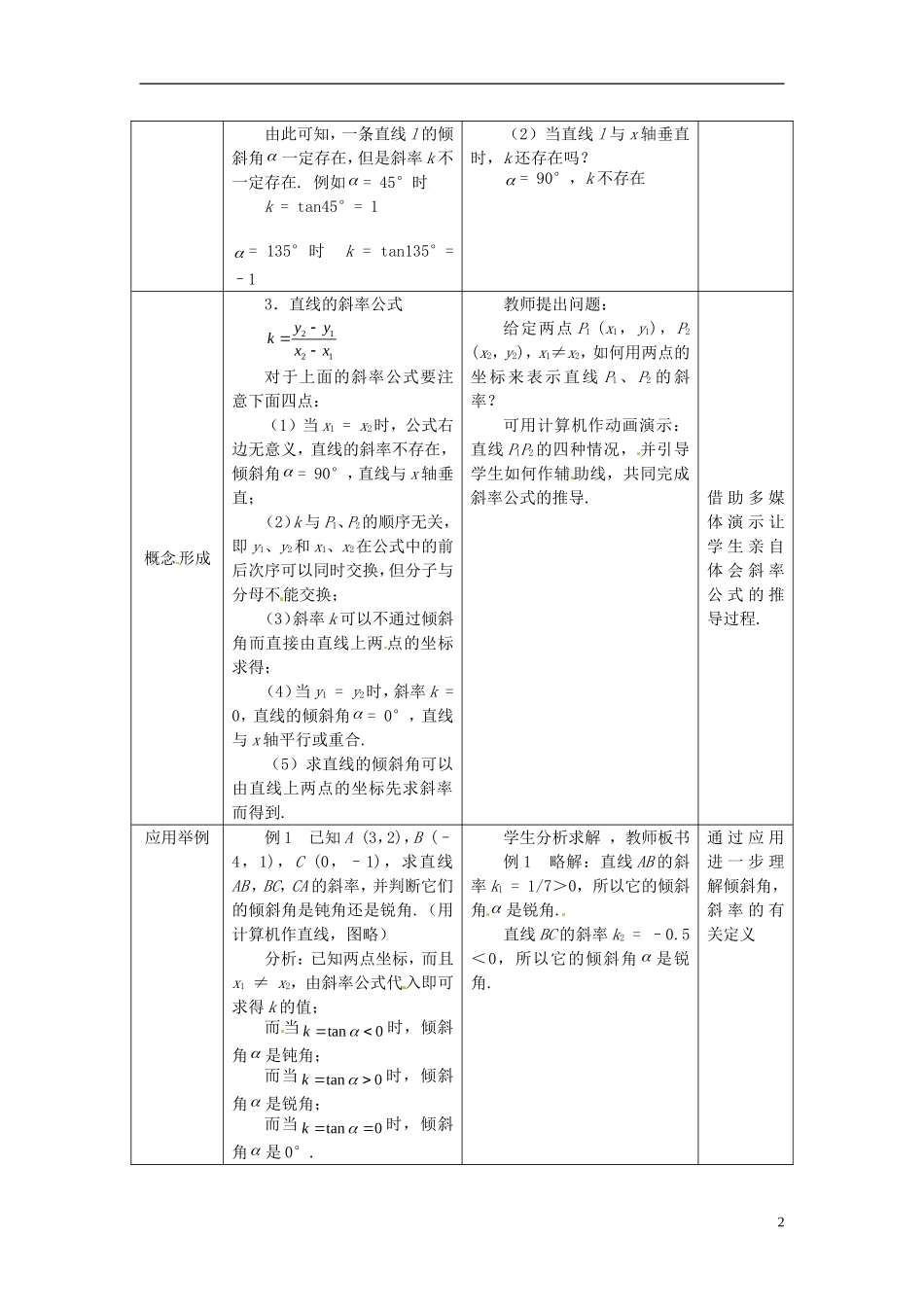
【新课教学过程设计(一)】第三章 直线与方程第 3.1.1 节倾斜角与斜率教学环节教学内容师生互动设计意图提出问题引入我们知道,经过两点有且只有(确定)一条直线,那么,经过一点 P 的直线 l 的位置能确定吗?如图,过一点 P 可作无数多条直线 a,b,c,…易见,答案是否定的,这些直线有什么联系呢?直线的倾斜角的概念.学生回答(不能确定)(1)它们都经过点 P.(2)它们的倾斜程度不同.接 着教师提出:怎样描述这种倾斜程度的不同?由此引入课题.设疑激趣导入课题概念形成1. 直线倾斜角的概念当直线 l 与 x 轴相交时,取x 轴作为基准,x 轴正向与直线l 向上方向之间所成的角 叫做直线 l 的倾斜角.特别地,当直线 l 与 x 轴平行或重合时,规定0 .教师提问:倾斜角 的取值范围是什么? 0180当 直 线 l 与 x 轴 重 合 时90 (由学生结合图形回答)概念深化因为平面直角坐标系内的每一条直线都有确定的倾斜程度,引入直线的倾斜角之后,我们就可以用倾斜角 来表示平面直角坐标系内的每一条直线的倾斜程度.确定平面直角坐标系内的一条直线位置的几何要素:一个点 P 和一个倾斜角 .教师提问:如左图,直线 a∥b∥c,那么它们的倾斜角 相等吗?学生回答后作出结论.一个倾斜角 不能确定一条直线,进而得出. 确定一条直线位置的几何要素.通 过这 种 师 生互 动 引 导学 生 明 确确 定 一 条直 线 位 置的 两 个 几何要素概念形成2.直线的斜率一条直线的倾斜角 ( ≠90°)的正切值叫做这条直线的斜率.斜率常用小写字母 k 表示,即tank.教师提问:(由学生讨论后回答)(1)当直线 l 与 x 轴平行或重合时,k 为多少?k = tan0°= 0 设疑激发学生思考得出结论1yabcxO由此可知,一条直线 l 的倾斜角 一定存在,但是斜率 k 不一定存在. 例如 = 45°时k = tan45°= 1 = 135°时 k = tan135°= –1 (2)当直线 l 与 x 轴垂直时,k 还存在吗? = 90°,k 不存在概念形成3.直线的斜率公式2121yykxx对于上面的斜率公式要注意下面四点:(1)当 x1 = x2时,公式右边无意义,直线的斜率不存在,倾斜角 = 90°,直线与 x 轴垂直;(2)k 与 P1、P2的顺序无关,即 y1、y2和 x1、x2在公式中的前后次序可以同时交换,但分子与分母不能交换;(3)斜率 k 可以不...