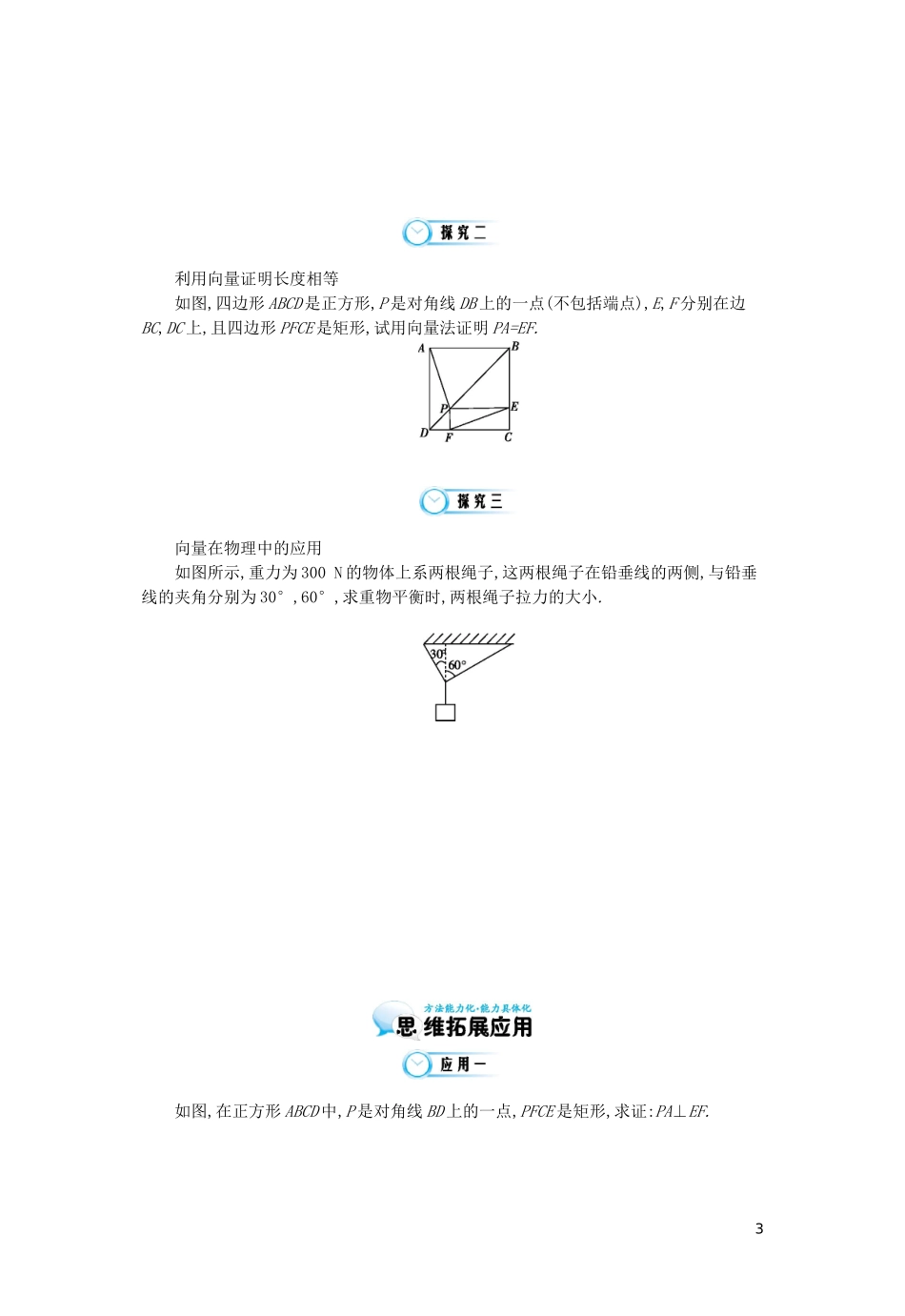
第 8 课时 平面向量应用举例1.能通过向量运算研究几何问题中点、线段、夹角之间的关系.2.会用向量知识解决一些物理问题.向量概念有明确的物理背景和几何背景,物理背景是力、速度、加速度等,几何背景是有向线段,可以说向量概念是从物理背景、几何背景中抽象而来的,正因为如此,利用向量可以解决一些物理和几何问题,在平面几何中,平行四边形是大家熟悉的重要的几何图形,而在物理中,受力分析则是其中最基础的知识,那么在本节的学习中,借助同学们非常熟悉的内容来学习向量在几何与物理问题中的应用.问题 1:利用向量法解决几何问题的一般步骤如何?向量法解决几何问题的“三步曲”.(1)建立平面几何与向量的联系,用向量表示问题中涉及的几何元素,把平面几何问题转化为向量问题;(2)通过向量运算,研究几何元素之间的关系;(3)把运算结果“翻译”成几何关系.问题 2:向量法可以解决几何中的哪些问题?平面几何中的距离(线段长度)、夹角、平行、垂直等都可以由向量的线性运算及数量积运算求得. 问题 3:向量在物理中的应用,其步骤如何?(1)建模:把物理问题转化为 问题; (2)解模:解答得到的数学问题;(3)回答:利用解得的数学答案解释 现象. 问题 4:如何应用向量知识解决力学问题和速度问题?应用向量知识解决力学问题,首先要对物体进行正确的 分析,画出受力分析图形,在此基础上转化为向量问题; 应用向量知识解决速度问题,首先要对物体运动的速度进行合理的合成与 ,结合运动学原理,转化为数学问题. 1.已知点 O 为三角形 ABC 所在平面内一点,若++=0,则点 O 是三角形 ABC 的( ).1A.重心 B.垂心 C.内心 D.外心2.如图所示,用两条成 120°角的等长的绳子悬挂一个灯具,已知灯具的重量为 10 N,则每根绳子的拉力大小是( ).A.5 NB.5 NC.10 ND.10 N3.若向量=(2,2),=(-2,3)分别表示两个力 F1,F2,则|F1+F2|= . 4.求证:平行四边形对角线互相平分.利用向量证明线段垂直在等腰直角三角形 ABC 中,AC=BC,D 是 BC 的中点,E 是 AB 上的点,且 AE=2BE,求证:AD⊥CE.2利用向量证明长度相等如图,四边形 ABCD 是正方形,P 是对角线 DB 上的一点(不包括端点),E,F 分别在边BC,DC 上,且四边形 PFCE 是矩形,试用向量法证明 PA=EF.向量在物理中的应用如图所示,重力为 300 N 的物体上系两根绳子,这两根绳子在铅垂线的两侧,与铅垂线的夹角分别为 30°,60°,求重物平衡时,两根绳子拉力的大小.如图,在正方形 ABCD 中,P 是对角线 BD 上的...