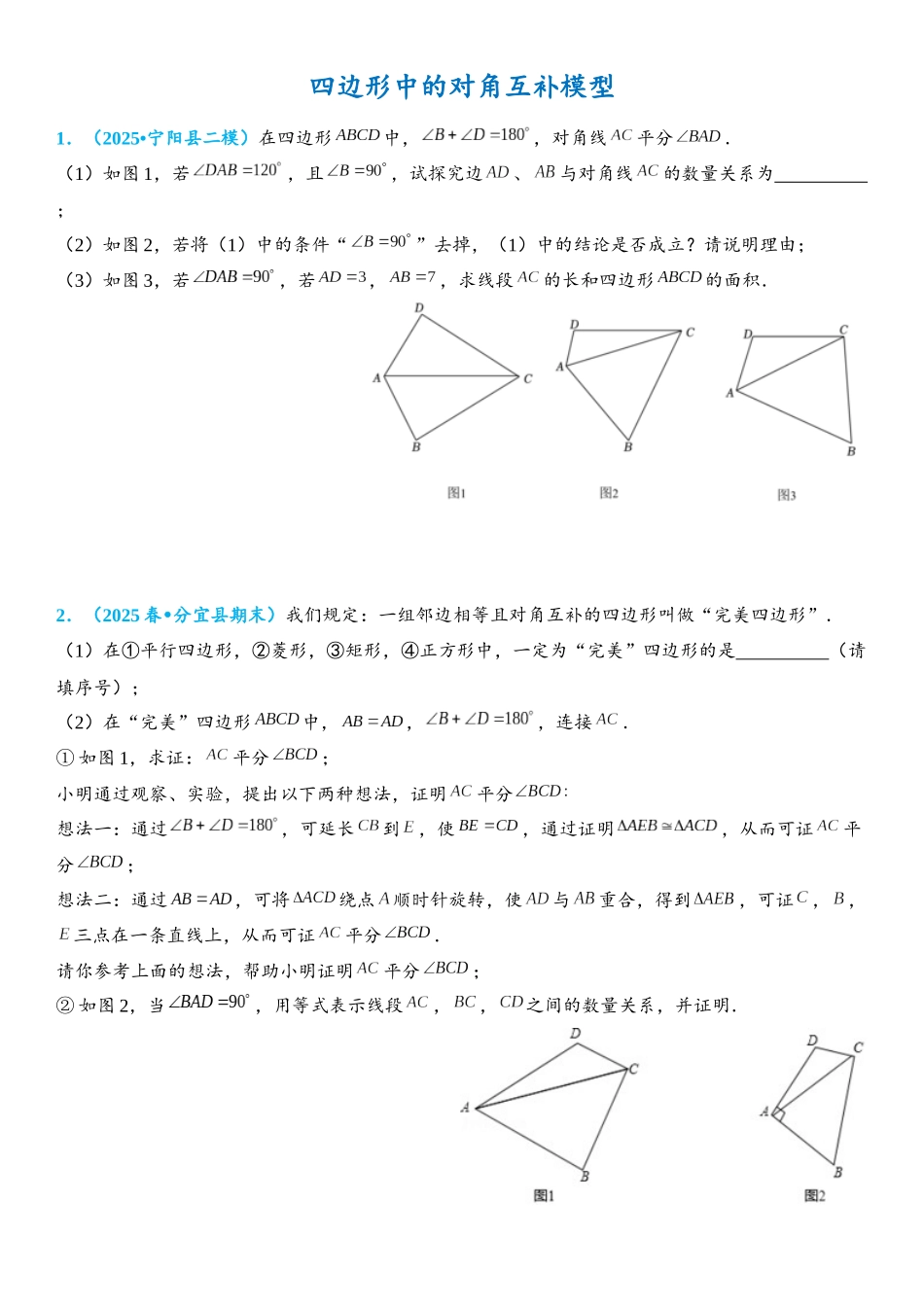
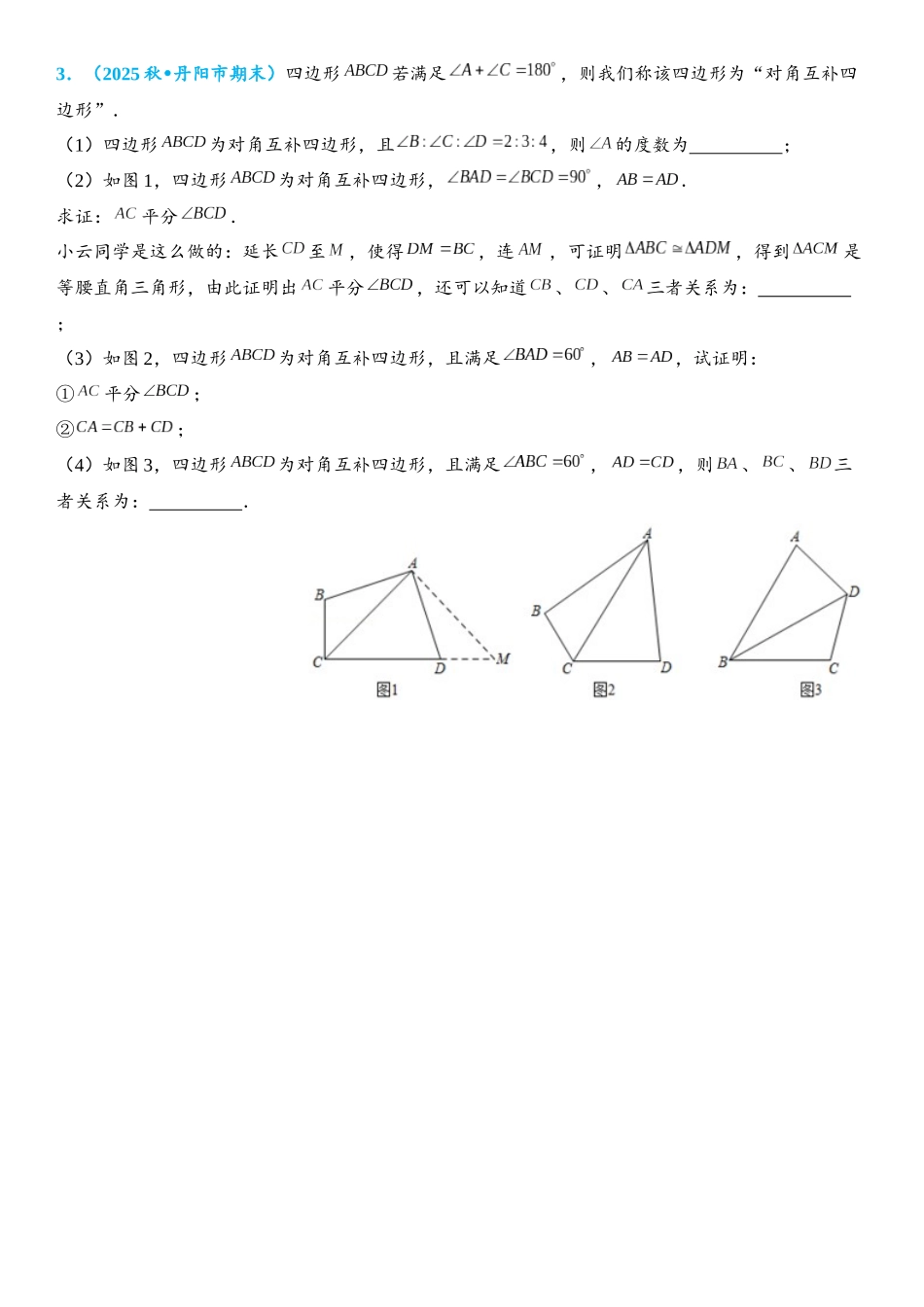
四边形中的对角互补模型1.(2025•宁阳县二模)在四边形中,,对角线平分.(1)如图 1,若,且,试探究边、与对角线的数量关系为 ;(2)如图 2,若将(1)中的条件“”去掉,(1)中的结论是否成立?请说明理由;(3)如图 3,若,若,,求线段的长和四边形的面积.2.(2025 春 分宜县期末)•我们规定:一组邻边相等且对角互补的四边形叫做“完美四边形”.(1)在①平行四边形,②菱形,③矩形,④正方形中,一定为“完美”四边形的是 (请填序号);(2)在“完美”四边形中,,,连接.① 如图 1,求证:平分;小明通过观察、实验,提出以下两种想法,证明平分想法一:通过,可延长到,使,通过证明,从而可证平分;想法二:通过,可将绕点顺时针旋转,使与重合,得到,可证,,三点在一条直线上,从而可证平分.请你参考上面的想法,帮助小明证明平分;② 如图 2,当,用等式表示线段,,之间的数量关系,并证明.3.(2025 秋 丹阳市期末)•四边形若满足,则我们称该四边形为“对角互补四边形”.(1)四边形为对角互补四边形,且,则的度数为 ;(2)如图 1,四边形为对角互补四边形,,.求证:平分.小云同学是这么做的:延长至,使得,连,可证明,得到是等腰直角三角形,由此证明出平分,还可以知道、、三者关系为: ;(3)如图 2,四边形为对角互补四边形,且满足,,试证明:①平分;②;(4)如图 3,四边形为对角互补四边形,且满足,,则、、三者关系为: .4.(2025 秋 碑林区校级期末)•同学们在第一次微课中听取了刘老师与杨老师关于面积等分线练习的讲评,小浩同学对此产生兴趣,上网又查到了长方形的一些性质:长方形的对角线相等且互相平分,对角线所在的直线是其一条面积等分线.请你利用以上性质,帮小浩解决下面问题:问题发现:(1)如图①,已知长方形,请画出它的一条面积等分线 (不经过对角线);问题探究:(2)四边形位于如图②所示的平面直角坐标系中,顶点位于原点,其余顶点坐标为,,,是四边形的一条面积等分线,点在轴上,请求出点的坐标.问题解决:(3)全民抗疫,西安加油!如图③,在平面直角坐标系中(长度单位为米),长方形是西安某小区在疫情期间为居民核酸检测围成的一个工作区域,顶点,在坐标轴上,为坐标原点,记顶点,原有的一个出入口在边上,且米.为使工作高效有序,现计划在边,,上依次再设出入口,,,沿,拉两道警戒线将工作区域分成面积相等的四部分....