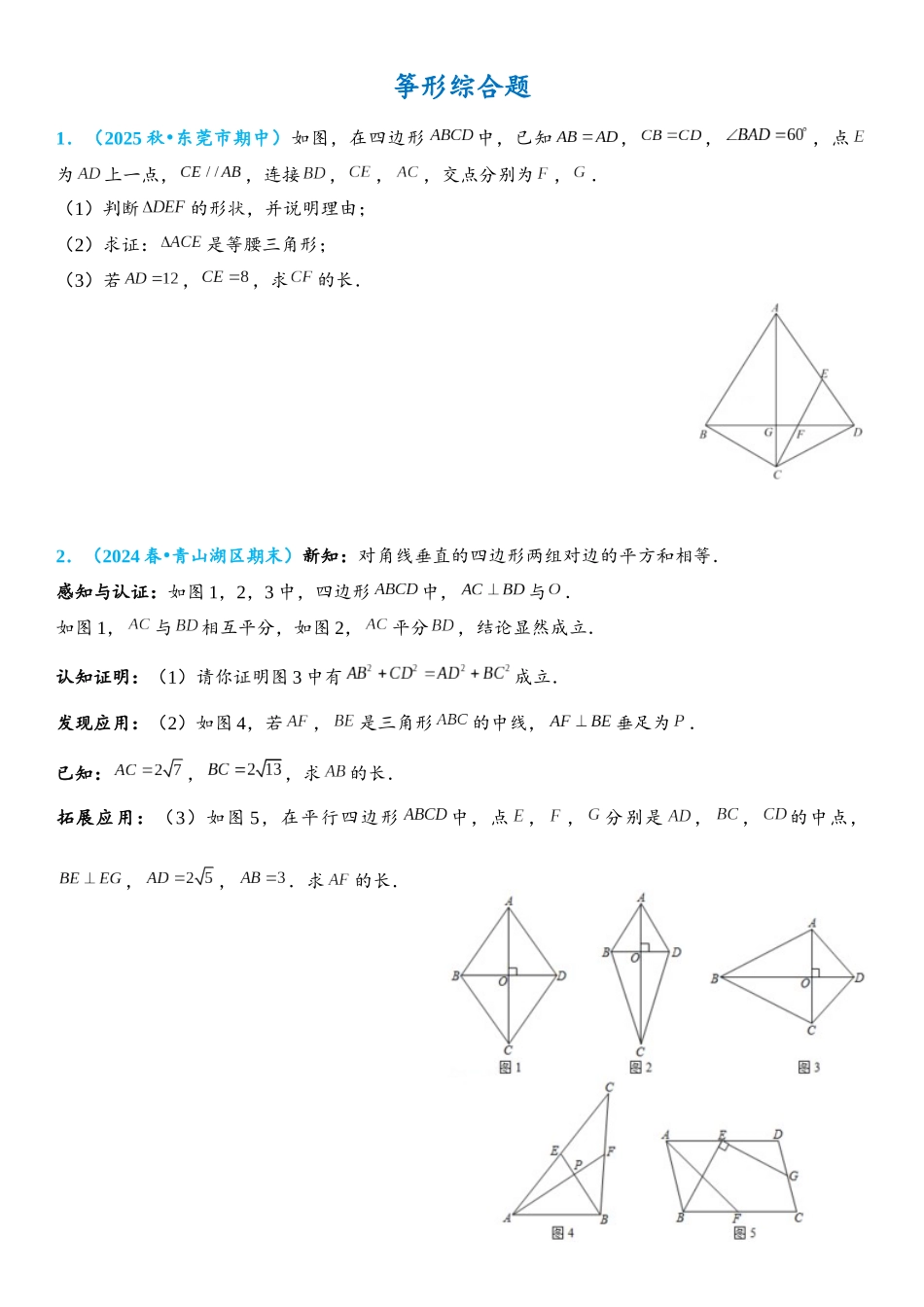
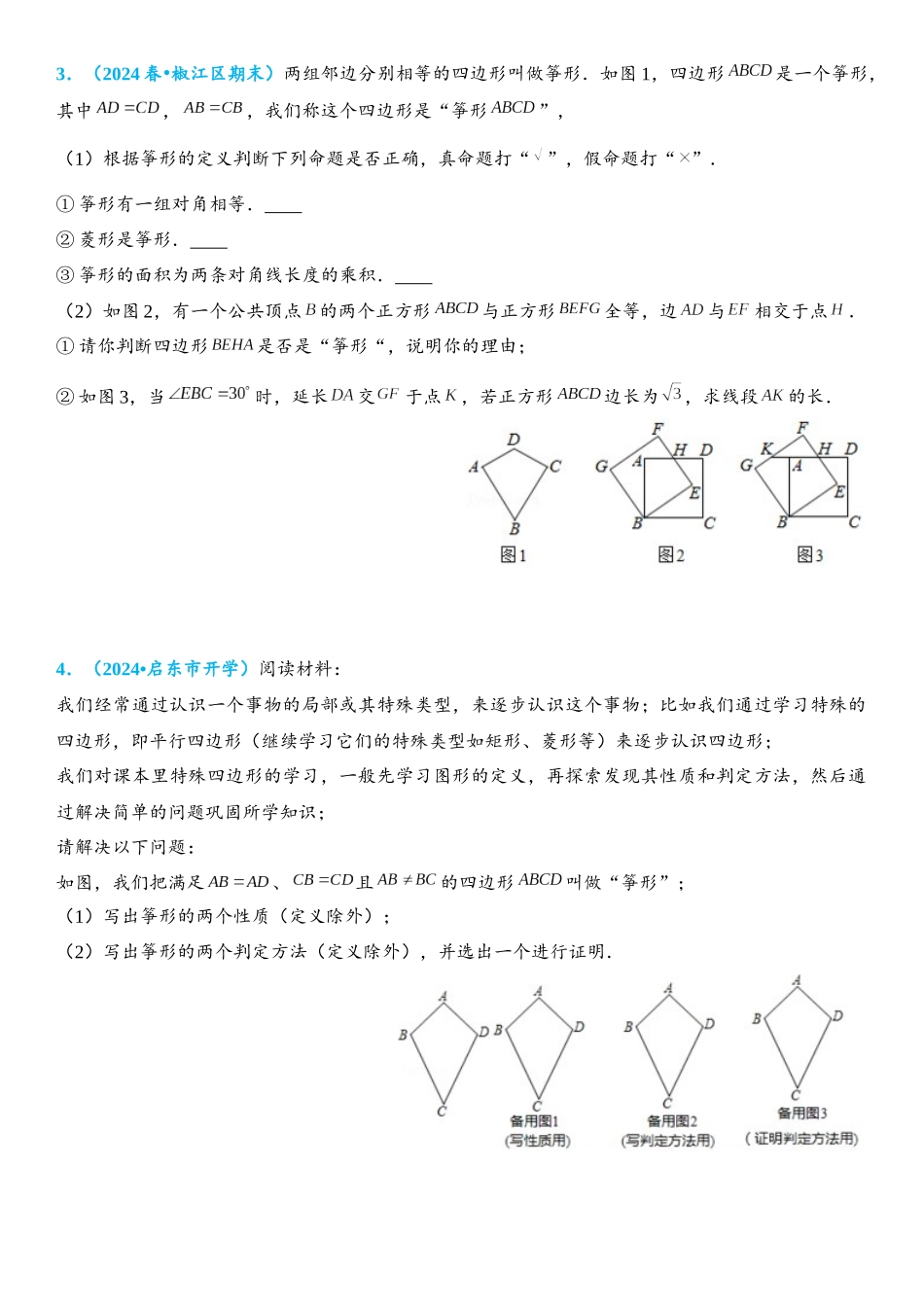
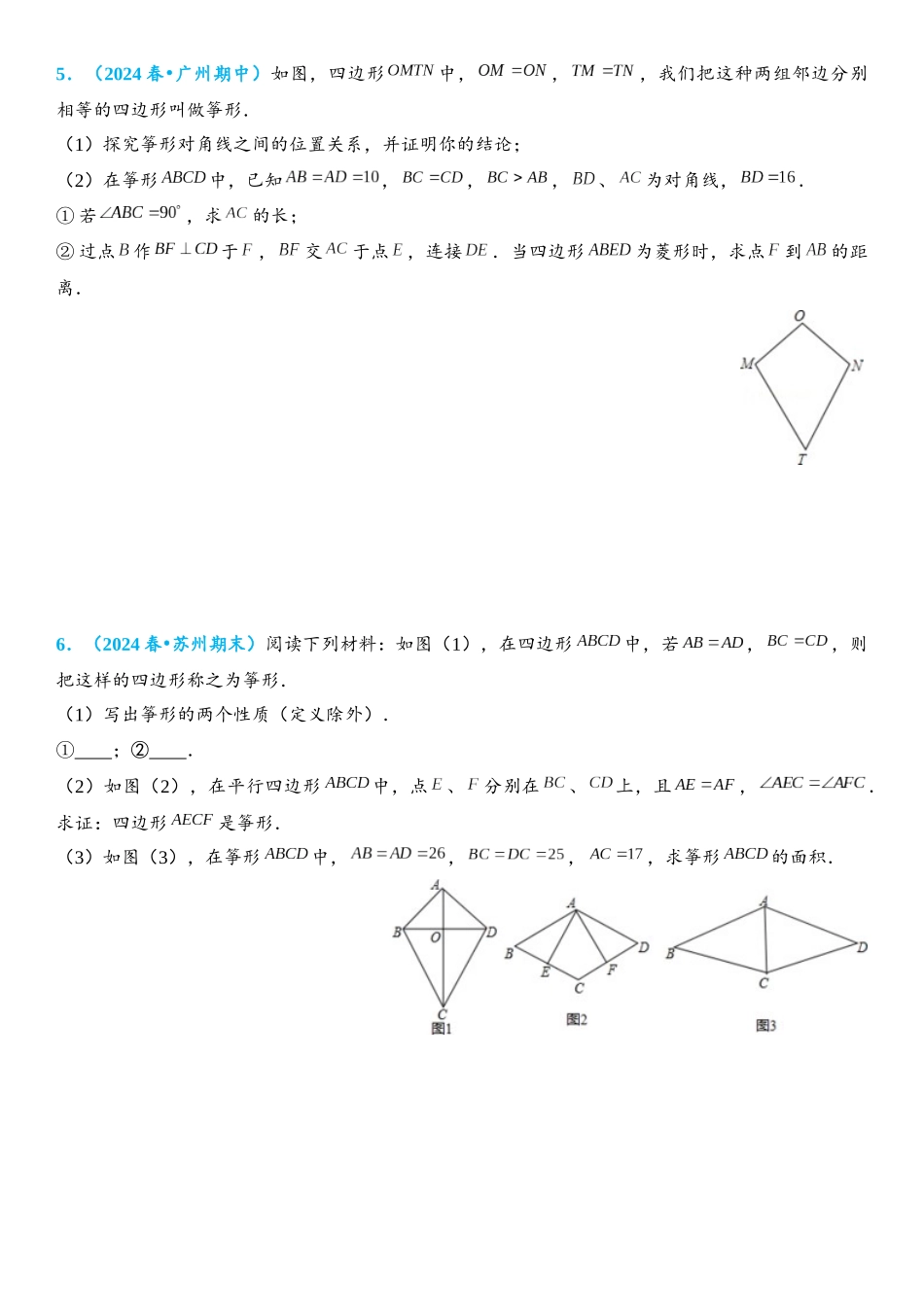
筝形综合题1.(2025 秋 东莞市期中)•如图,在四边形中,已知,,,点为上一点,,连接,,,交点分别为,.(1)判断的形状,并说明理由;(2)求证:是等腰三角形;(3)若,,求的长.2.(2024 春 青山湖区期末)•新知:对角线垂直的四边形两组对边的平方和相等.感知与认证:如图 1,2,3 中,四边形中,与.如图 1,与相互平分,如图 2,平分,结论显然成立.认知证明:(1)请你证明图 3 中有成立.发现应用:(2)如图 4,若,是三角形的中线,垂足为.已知:,,求的长.拓展应用:(3)如图 5,在平行四边形中,点,,分别是,,的中点,,,.求的长.3.(2024 春 椒江区期末)•两组邻边分别相等的四边形叫做筝形.如图 1,四边形是一个筝形,其中,,我们称这个四边形是“筝形”,(1)根据筝形的定义判断下列命题是否正确,真命题打“”,假命题打“ ”.① 筝形有一组对角相等. ② 菱形是筝形. ③ 筝形的面积为两条对角线长度的乘积. (2)如图 2,有一个公共顶点的两个正方形与正方形全等,边与相交于点.① 请你判断四边形是否是“筝形“,说明你的理由;② 如图 3,当时,延长交于点,若正方形边长为,求线段的长.4.(2024•启东市开学)阅读材料:我们经常通过认识一个事物的局部或其特殊类型,来逐步认识这个事物;比如我们通过学习特殊的四边形,即平行四边形(继续学习它们的特殊类型如矩形、菱形等)来逐步认识四边形;我们对课本里特殊四边形的学习,一般先学习图形的定义,再探索发现其性质和判定方法,然后通过解决简单的问题巩固所学知识;请解决以下问题:如图,我们把满足、且的四边形叫做“筝形”;(1)写出筝形的两个性质(定义除外);(2)写出筝形的两个判定方法(定义除外),并选出一个进行证明.5.(2024 春 广州期中)•如图,四边形中,,,我们把这种两组邻边分别相等的四边形叫做筝形.(1)探究筝形对角线之间的位置关系,并证明你的结论;(2)在筝形中,已知,,,、为对角线,.① 若,求的长;② 过点作于,交于点,连接.当四边形为菱形时,求点到的距离.6.(2024 春 苏州期末)•阅读下列材料:如图(1),在四边形中,若,,则把这样的四边形称之为筝形.(1)写出筝形的两个性质(定义除外).① ;② .(2)如图(2),在平行四边形中,点、分别在、上,且,.求证:四边形是筝形.(3)如图(3),在筝形中,,,,求筝形的面积.7.(2024...