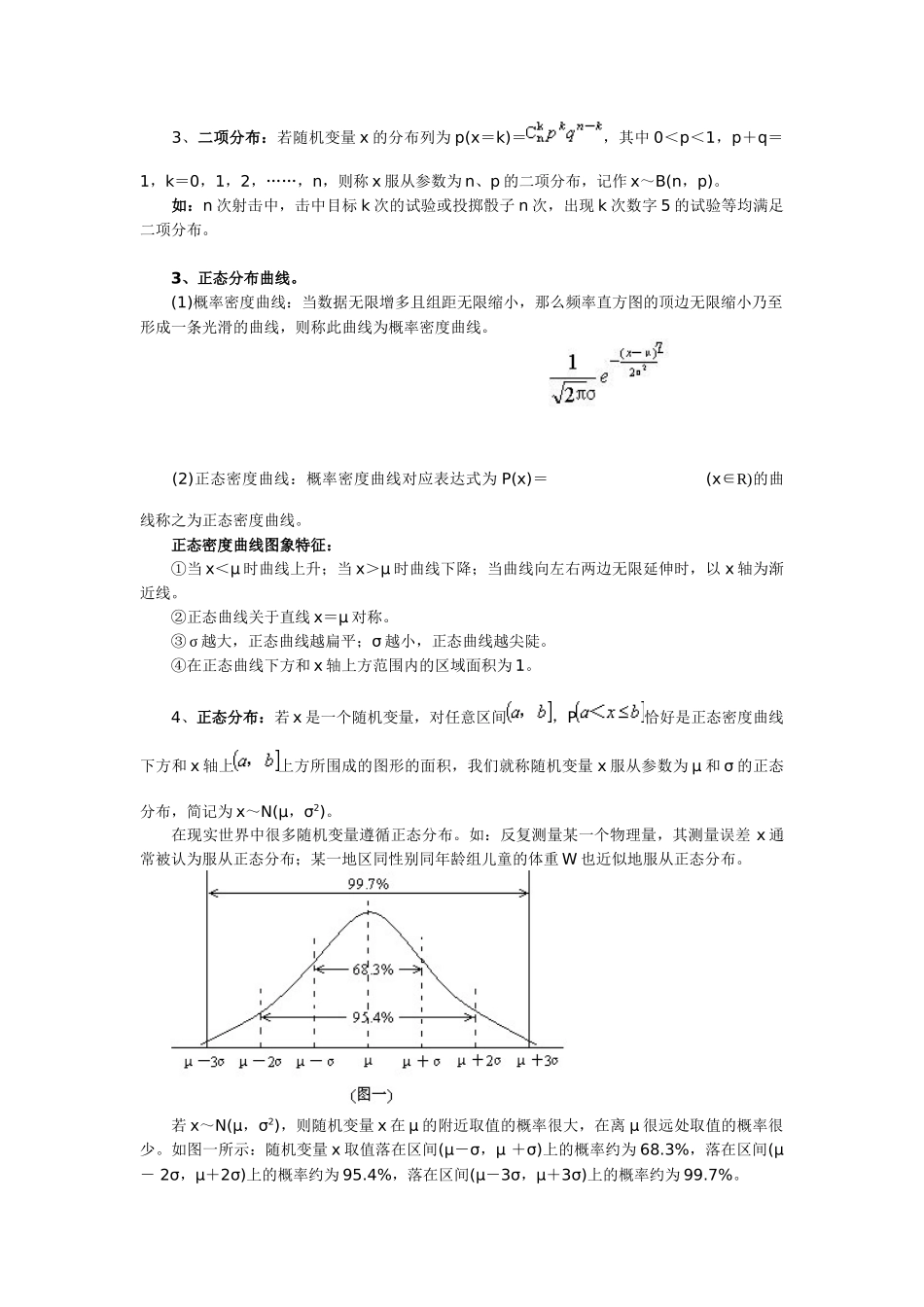
超几何分布、二项分布、正态分布 【学习目标】 1、通过实例,理解超几何分布及其特点,掌握超几何分布列及其导出过程,并能进行简单的应用。 2、理解 n 次独立重复试验(即 n 重伯努利试验)及其意义,理解二项分布并能解决一些简单的实际问题。 3、借助直观图,了解是正态分布曲线与正态分布,认识正态分布曲线的特点及曲线表示的意义。 4、会查标准正态分布表,会求满足正态分布的随机变量 x 在某一范围内的概率。 【重点与难点】 重点:正确理解超几何分布、二项分布、正态分布的意义。 难点:正确进行超几何分布、二项分布、正态分布有关概率的计算。 【知识要点】 1、超几何分布: 一般地,若一个随机变量 x 的分布列为:P(x=r)= ① 其中 r=0,1,2,3,…… , , =min(n,M),则称 x 服从超几何分布。 记作 x~H(n,M,N),并将 P(x=r)=,记为 H(r,n,M,N)。 如:在一批数量为 N 件的产品中共有 M 件不合格品,从中随机取出的 n 件产品中,不合格品数 x 的概率分布列如表一所示: (表一) 其中 =min(n,M),满足超几何分布。 2、伯努利试验(n 次独立重复试验),在 n 次相互独立试验中,每次试验的结果仅有两种对立的结果 A 与出现,P(A)=p∈(0,1),这样的试验称为 n 次独立重复试验,也称为伯努利试验。 P()=1-p=q,则在 n 次独立重复试验中,事件 A 恰好发生 k 次的概率(0≤k≤n)为P(k)=(k=0,1,2,3,……,n),它恰好是(q+p)n的二项展开式中的第 k+1 项。 3、二项分布:若随机变量 x 的分布列为 p(x=k)=,其中 0<p<1,p+q=1,k=0,1,2,……,n,则称 x 服从参数为 n、p 的二项分布,记作 x~B(n,p)。 如:n 次射击中,击中目标 k 次的试验或投掷骰子 n 次,出现 k 次数字 5 的试验等均满足二项分布。 3、正态分布曲线。 (1)概率密度曲线:当数据无限增多且组距无限缩小,那么频率直方图的顶边无限缩小乃至形成一条光滑的曲线,则称此曲线为概率密度曲线。 (2)正态密度曲线:概率密度曲线对应表达式为 P(x)=(x∈R)的曲线称之为正态密度曲线。 正态密度曲线图象特征: ①当 x<μ 时曲线上升;当 x>μ 时曲线下降;当曲线向左右两边无限延伸时,以 x 轴为渐近线。 ②正态曲线关于直线 x=μ 对称。 ③ σ 越大,正态曲线越扁平;σ 越小,正态曲线越尖陡。 ④在正态曲线下方和 x 轴上方范围内的区域...