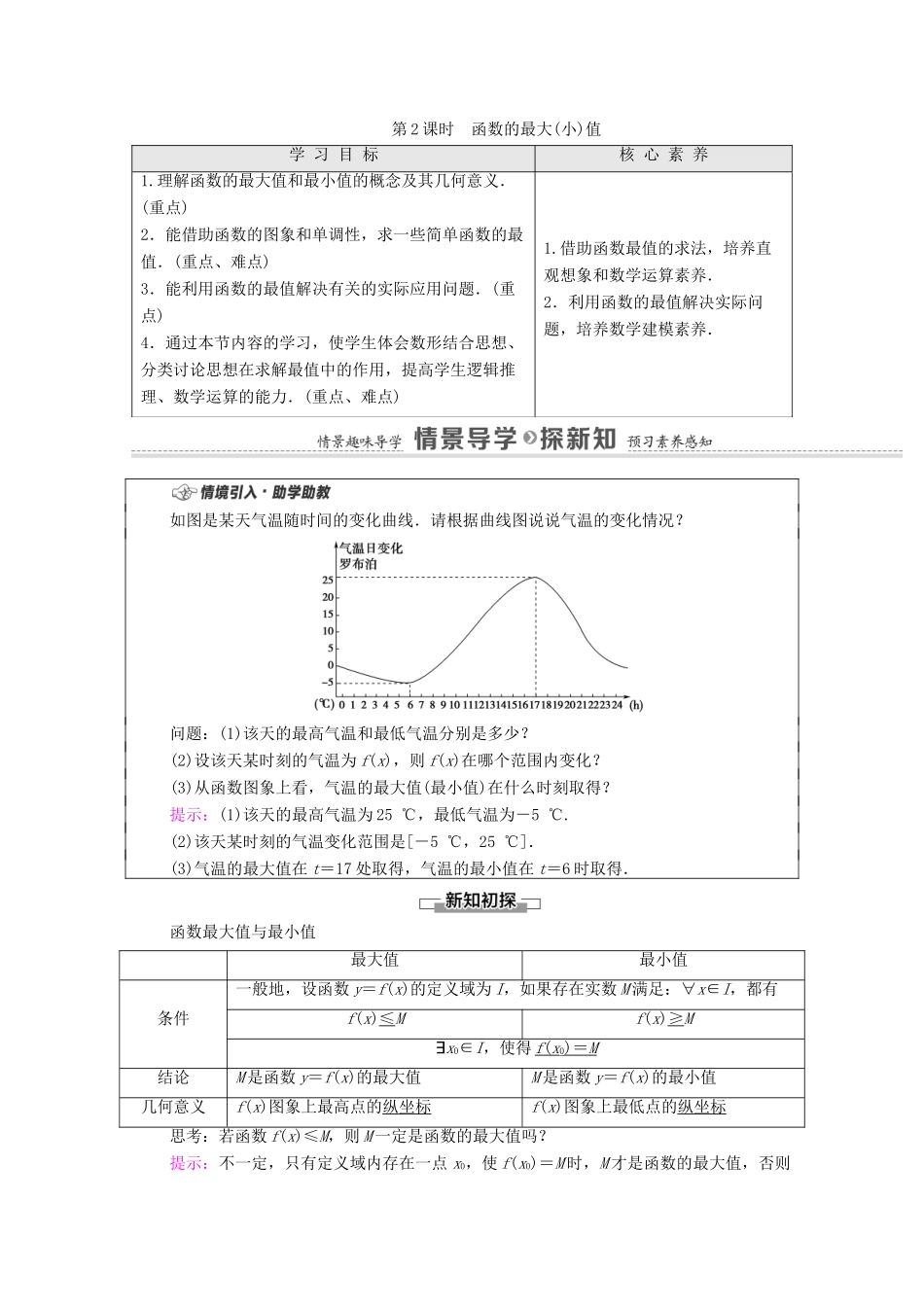
第 2 课时 函数的最大(小)值学 习 目 标核 心 素 养1.理解函数的最大值和最小值的概念及其几何意义.(重点)2.能借助函数的图象和单调性,求一些简单函数的最值.(重点、难点)3.能利用函数的最值解决有关的实际应用问题.(重点)4.通过本节内容的学习,使学生体会数形结合思想、分类讨论思想在求解最值中的作用,提高学生逻辑推理、数学运算的能力.(重点、难点)1.借助函数最值的求法,培养直观想象和数学运算素养.2.利用函数的最值解决实际问题,培养数学建模素养.如图是某天气温随时间的变化曲线.请根据曲线图说说气温的变化情况?问题:(1)该天的最高气温和最低气温分别是多少?(2)设该天某时刻的气温为 f(x),则 f(x)在哪个范围内变化?(3)从函数图象上看,气温的最大值(最小值)在什么时刻取得?提示:(1)该天的最高气温为 25 ℃,最低气温为-5 ℃.(2)该天某时刻的气温变化范围是[-5 ℃,25 ℃].(3)气温的最大值在 t=17 处取得,气温的最小值在 t=6 时取得.函数最大值与最小值最大值最小值条件一般地,设函数 y=f(x)的定义域为 I,如果存在实数 M 满足:∀x∈I,都有f(x)≤Mf(x)≥M∃x0∈I,使得 f ( x 0) = M 结论M 是函数 y=f(x)的最大值M 是函数 y=f(x)的最小值几何意义f(x)图象上最高点的纵坐标f(x)图象上最低点的纵坐标思考:若函数 f(x)≤M,则 M 一定是函数的最大值吗?提示:不一定,只有定义域内存在一点 x0,使 f(x0)=M 时,M 才是函数的最大值,否则不是.1.思考辨析(正确的画“√”,错误的画“×”)(1)任何函数都有最大(小)值.( )(2)函数 f(x)在[a,b]上的最值一定是 f(a)(或 f(b)).( )(3)函数的最大值一定比最小值大.( )[答案] (1)× (2)× (3)√2.函数 y=f(x)在[-2,2]上的图象如图所示,则此函数的最小值、最大值分别是 ( )A.-1,0B.0,2C.-1,2D.,2C [由图可知,f(x)的最大值为 f(1)=2,f(x)的最小值为 f(-2)=-1.]3.设函数 f(x)=2x-1(x<0),则 f(x)( )A.有最大值 B.有最小值C.既有最大值又有最小值 D.既无最大值又无最小值D [ f(x)在(-∞,0)上单调递增,∴f(x)