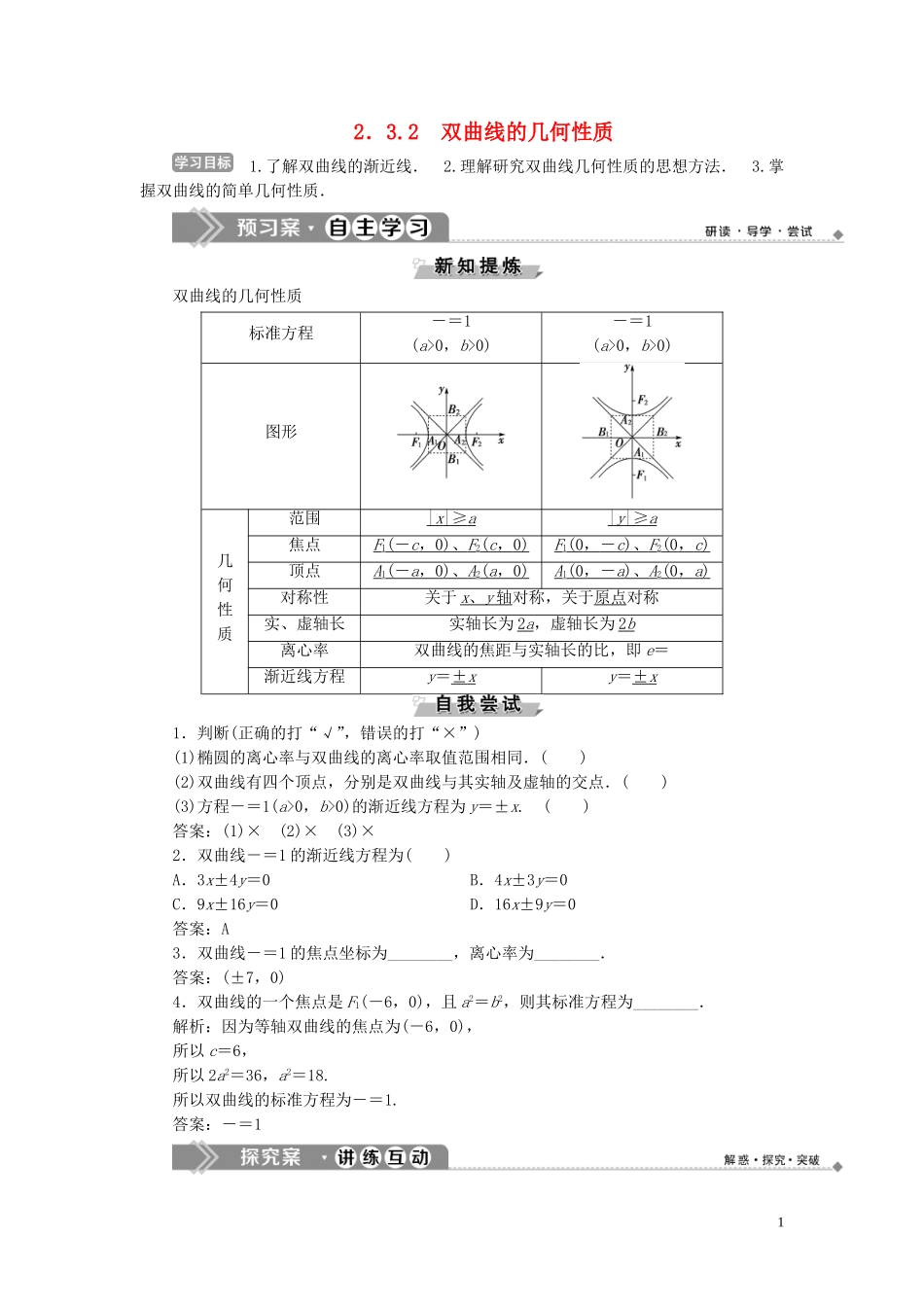
2.3.2 双曲线的几何性质 1.了解双曲线的渐近线. 2.理解研究双曲线几何性质的思想方法. 3.掌握双曲线的简单几何性质.双曲线的几何性质标准方程-=1(a>0,b>0)-=1(a>0,b>0)图形几何性质范围| x |≥ a | y |≥ a 焦点F1( - c , 0 ) 、 F 2( c , 0 ) F1(0 , - c ) 、 F 2(0 , c ) 顶点A1( - a , 0 ) 、 A 2( a , 0 ) A1(0 , - a ) 、 A 2(0 , a ) 对称性关于 x 、 y 轴 对称,关于原点对称实、虚轴长实轴长为 2 a ,虚轴长为 2 b 离心率双曲线的焦距与实轴长的比,即 e=渐近线方程y=± x y=± x 1.判断(正确的打“√”,错误的打“×”)(1)椭圆的离心率与双曲线的离心率取值范围相同.( )(2)双曲线有四个顶点,分别是双曲线与其实轴及虚轴的交点.( )(3)方程-=1(a>0,b>0)的渐近线方程为 y=±x. ( )答案:(1)× (2)× (3)×2.双曲线-=1 的渐近线方程为( )A.3x±4y=0 B.4x±3y=0C.9x±16y=0 D.16x±9y=0答案:A3.双曲线-=1 的焦点坐标为________,离心率为________.答案:(±7,0) 4.双曲线的一个焦点是 F1(-6,0),且 a2=b2,则其标准方程为________.解析:因为等轴双曲线的焦点为(-6,0),所以 c=6,所以 2a2=36,a2=18.所以双曲线的标准方程为-=1.答案:-=11 双曲线的简单几何性质 求双曲线 9y2-4x2=-36 的顶点坐标、焦点坐标、实轴长、虚轴长、离心率和渐近线方程.【解】 将 9y2-4x2=-36 变形为-=1,即-=1,所以 a=3,b=2,c=,因此顶点坐标为(-3,0),(3,0),焦点坐标为(-,0),(,0),实轴长是 2a=6,虚轴长是 2b=4,离心率 e==,渐近线方程 y=±x. 把本例中的双曲线方程改为 9y2-4x2=36,再求顶点坐标、焦点坐标、离心率、渐近线方程.解:把方程 9y2-4x2=36 化为标准形式为-=1,所以 a=2,b=3,c=,所以顶点坐标为(0,-2),(0,2),焦点坐标为(0,-),(0,),离心率 e==.渐近线方程为 y=±x.由双曲线的标准方程求几何性质的四个步骤 1.双曲线 x2-y2=1 的顶点到其渐近线的距离等于( )A. B.C.1 D.解析:选 B.双曲线 x2-y2=1 的顶点坐标为(±1,0),渐近线为 y=±x,所以 x±y=0,所以顶点到渐近线的距离为 d==.2.已知 F1,F2分别是双曲线的左,右焦点,P 为该双曲线上一点,若△PF1F2为等腰直角三角...