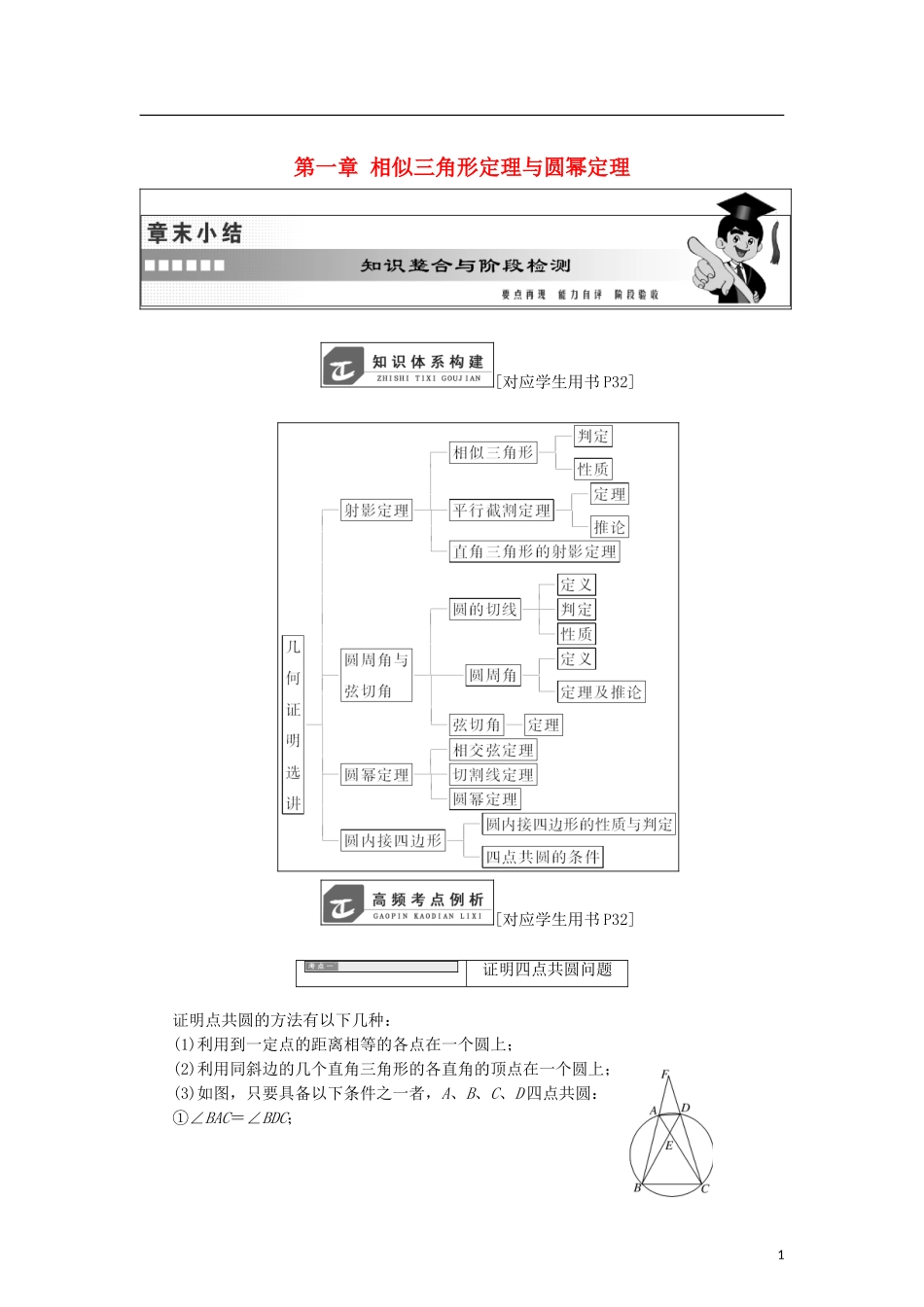
第一章 相似三角形定理与圆幂定理[对应学生用书 P32][对应学生用书 P32]证明四点共圆问题证明点共圆的方法有以下几种:(1)利用到一定点的距离相等的各点在一个圆上;(2)利用同斜边的几个直角三角形的各直角的顶点在一个圆上;(3)如图,只要具备以下条件之一者,A、B、C、D 四点共圆:①∠BAC=∠BDC;1②∠BAD+∠BCD=180°;③∠FAD=∠BCD;④AE·CE=BE·DE;⑤AF·BF=CF·DF.[例 1] 已知四边形 ABCD 为平行四边形,过点 A 和点 B 的圆与 AD、BC 分别交于 E、F,求证:C、D、E、F 四点共圆.[证明] 连接 EF,因为四边形 ABCD 为平行四边形,所以∠B+∠C=180°.因为四边形 ABFE 内接于圆,所以∠B+∠AEF=180°.所以∠AEF=∠C.所以 C、D、E、F 四点共圆.[例 2] 已知:如图,四边形 ABCD 中,∠1=∠2.求证:A、B、C、D 四点共圆.[证明] 由 A、B、D 三点可以确定一个圆,设该圆为⊙O.(1)如果点 C 在⊙O 的外部(如图).与圆相交于点 E, ∠1=∠AEB,∠1=∠2,∴∠2=∠AEB.而∠AEB>∠2,矛盾,故点 C 不可能在圆外.(2)如果点 C 在⊙O 的内部(如图).延长 BC 与圆相交于点 E,连接 AE.则∠1=∠AEB,而∠1=∠2,∴∠2=∠AEB,与∠2>∠AEB 矛盾,∴点 C 不可能在圆内,∴点 C 只能在圆上.证明线段等积式常用的方法证明命题的一般步骤:(1)弄清题意,辨明题设和结论;(2)用分析法探明证题思路和方法;(3)若已知条件不足,可添设适当辅助线以暴露隐含的已知条件;(4)用综合法有条理地写出证明过程;(5)检查证明过程的合理性.21.利用相似三角形[例 3] 如图,⊙O 和⊙O′相交于 A,B 两点,过 A 作两圆的切线分别交两圆于 C,D 两点,连结 DB 并延长交⊙O 于点 E.证明:(1)AC·BD=AD·AB;(2)AC=AE.[证明] (1)由 AC 与⊙O′相切于 A,得∠CAB=∠ADB,同理∠ACB=∠DAB,所以△ACB∽△DAB.从而=,即 AC·BD=AD·AB.(2)由 AD 与⊙O 相切于 A,得∠AED=∠BAD,又∠ADE=∠BDA,得△EAD∽△ABD.从而=,即 AE·BD=AD·AB.结合(1)的结论,得 AC=AE.2.利用三角形内(外)角平分线的性质[例 4] 已知 C 点在圆 O 直径 BE 的延长线上,CA 切圆 O 于 A点,DC 是∠ACB 的平分线交 AE 于点 F,交 AB 于 D 点.(1)求∠ADF 的度数;(2)若 AB=AC,求 AC∶BC.[解] (1) AC 为圆 O 的切线,∴∠B=∠EAC.又 DC 是∠ACB 的平分线,∴∠...