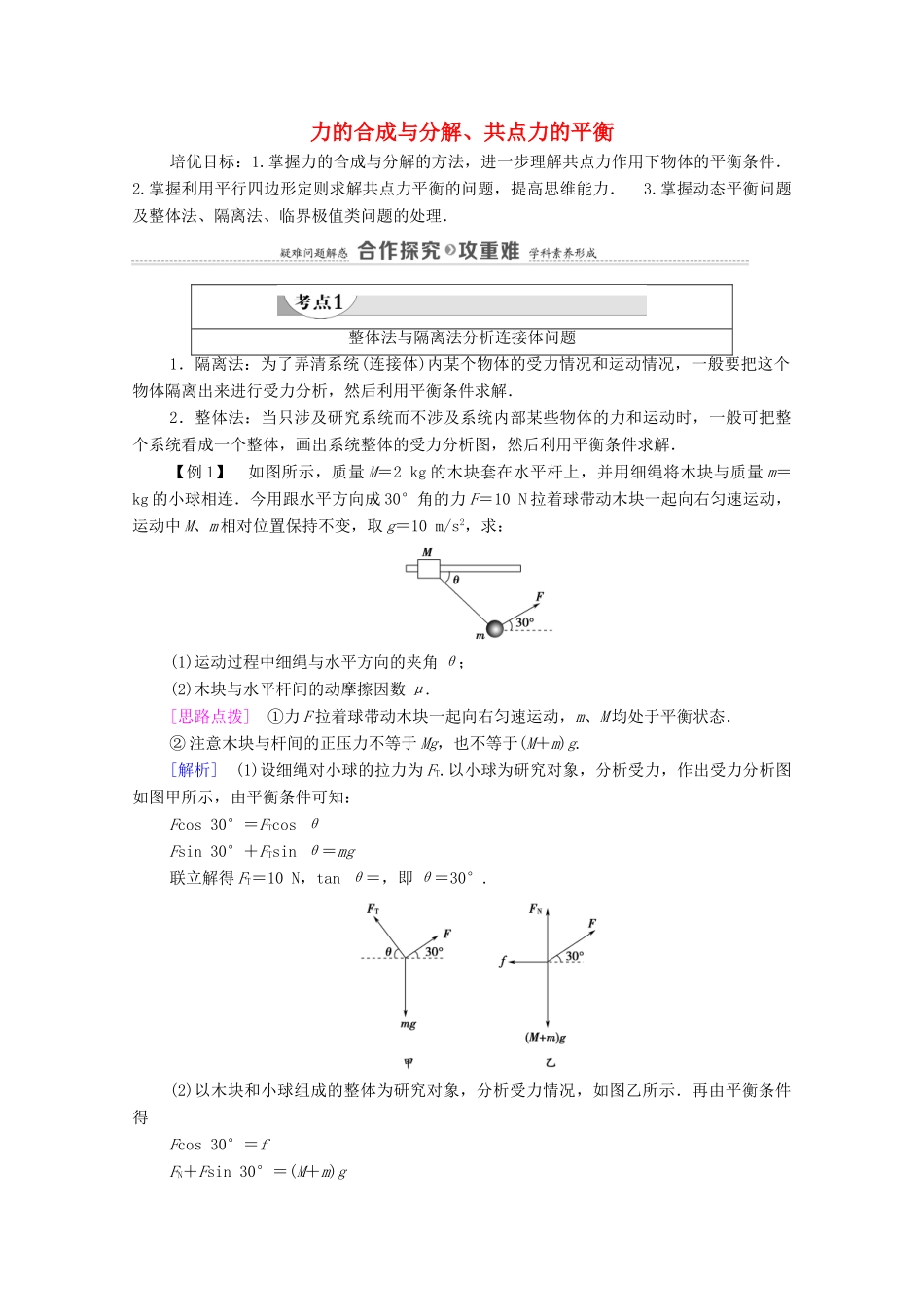
力的合成与分解、共点力的平衡培优目标:1.掌握力的合成与分解的方法,进一步理解共点力作用下物体的平衡条件. 2.掌握利用平行四边形定则求解共点力平衡的问题,提高思维能力. 3.掌握动态平衡问题及整体法、隔离法、临界极值类问题的处理.整体法与隔离法分析连接体问题1.隔离法:为了弄清系统(连接体)内某个物体的受力情况和运动情况,一般要把这个物体隔离出来进行受力分析,然后利用平衡条件求解.2.整体法:当只涉及研究系统而不涉及系统内部某些物体的力和运动时,一般可把整个系统看成一个整体,画出系统整体的受力分析图,然后利用平衡条件求解.【例 1】 如图所示,质量 M=2 kg 的木块套在水平杆上,并用细绳将木块与质量 m= kg 的小球相连.今用跟水平方向成 30°角的力 F=10 N 拉着球带动木块一起向右匀速运动,运动中 M、m 相对位置保持不变,取 g=10 m/s2,求:(1)运动过程中细绳与水平方向的夹角 θ;(2)木块与水平杆间的动摩擦因数 μ.[思路点拨] ①力 F 拉着球带动木块一起向右匀速运动,m、M 均处于平衡状态.② 注意木块与杆间的正压力不等于 Mg,也不等于(M+m)g.[解析] (1)设细绳对小球的拉力为 FT.以小球为研究对象,分析受力,作出受力分析图如图甲所示,由平衡条件可知:Fcos 30°=FTcos θFsin 30°+FTsin θ=mg联立解得 FT=10 N,tan θ=,即 θ=30°.(2)以木块和小球组成的整体为研究对象,分析受力情况,如图乙所示.再由平衡条件得Fcos 30°=fFN+Fsin 30°=(M+m)g又 f=μFN得到 μ=代入解得 μ=.[答案] (1)30° (2)应用整体法与隔离法解连接体平衡问题应注意以下两点1 整体法分析时不考虑系统内物体间的相互作用力.2 隔离法分析时应考虑隔离受力个数较少的物体.[跟进训练]1.如图所示,用完全相同的轻弹簧 A、B、C 将两个相同的小球连接并悬挂,小球处于静止状态,弹簧 A 与竖直方向的夹角为 30°,弹簧 C 水平,则弹簧 A、C 的伸长量之比为( )A.∶4 B.4∶C.1∶2D.2∶1D [将两小球及弹簧 B 视为整体进行受力分析,有FC=FAsin 30°FC=kxCFA=kxA==2∶1=2∶1故 D 正确,A、B、C 错误.]动态平衡问题1.动态平衡:是指平衡问题中的一部分力是变力,是动态力,力的大小和方向均要发生变化,所以叫动态平衡,这是力平衡问题中的一类难题.2.基本思路:化“动”为“静”,“静”中求“动”.3.基本方法:图解法、解...