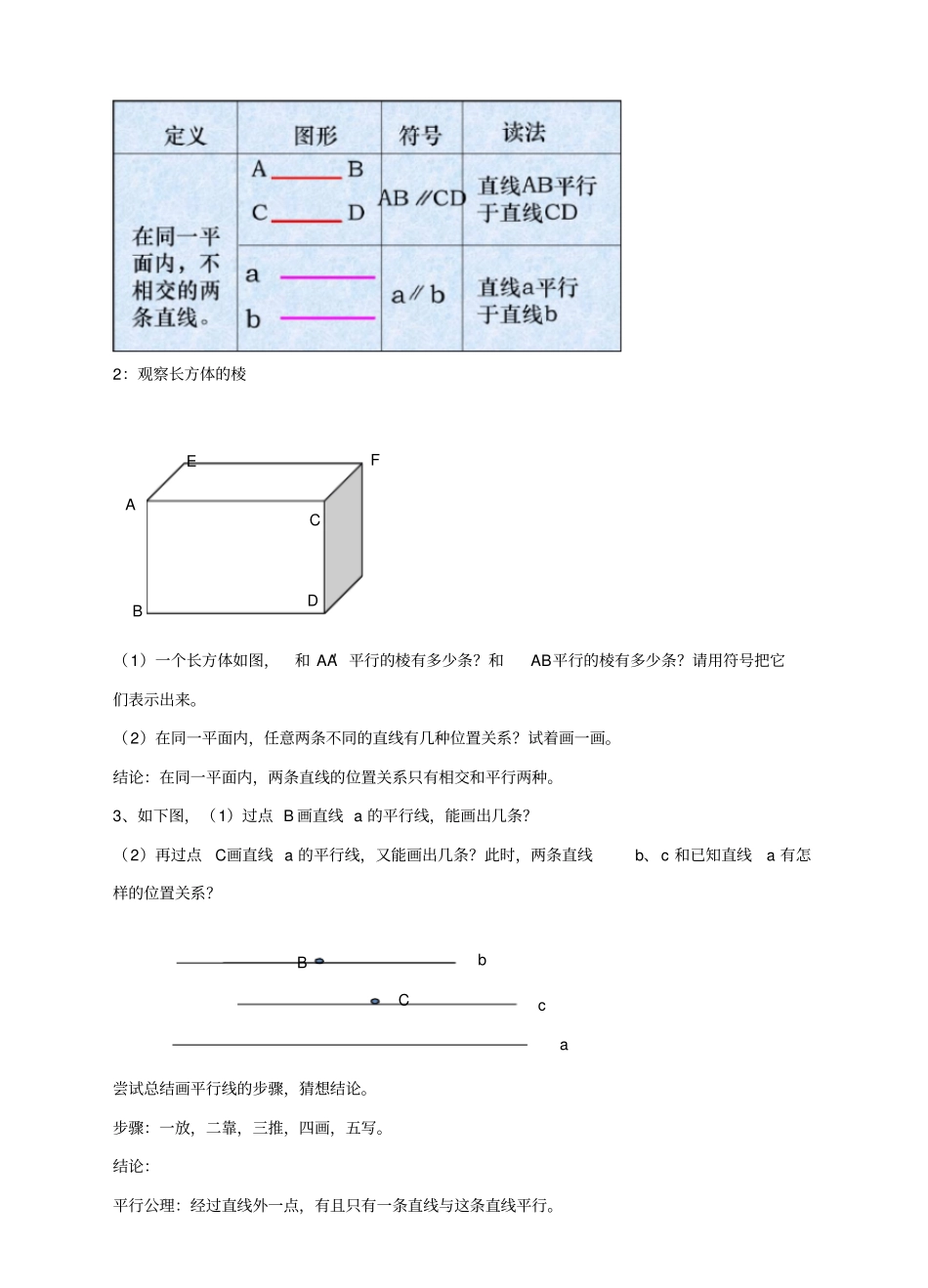
《平行线》精品教案教学目标1.掌握平行线的概念。知道平行线的表示方法。2.经过直线外一点会画已知直线的平行线。3.掌握平行公理及推论。重点、难点重点:平行公理及推论的理解。难点:对平行线概念的理解和平行线的画法。教学过程一、情境导入(多媒体展示)如图,分别将木条a、b与木条c钉在一起,并把它们想象成两端可以无限延伸的三条直线。转动a,直线a从在c的左侧与直线b相交逐步变为在右侧与b相交。想象一下,在这个过程中,有没有直线a与直线b不相交的位置呢?在木条转动观察中,有没有a与b不相交的位置呢?启发学生发挥想象力,想象成是向两方无限延伸的情形。在同一平面内,两条直线除了相交关系外,还有不相交的情况。引出课题——平行线。设计意图:通过学生熟悉的事物,直观形象地给出了生活中的平行线,利用演示实验,让学生更加直观的发现平行的现象,激发了学生的学习兴趣。二、探究新知1:举生活中平行线的实例同学们还能举出什么例子?总结:同一平面内.....,不相交的两条直线....叫做平行线。想一想:不平行的两条直线一定相交吗?注意:平行线的定义包含三层意思:(1)“在同一平面内”是前提条件,(2)“不相交”就是说两条直线没有交点,(3)平行线指的是“两条直线”而不是两条射线或两条线段.如何用几何语言描述平行呢?我们通常用符号“//”表示平行。平行线的表示2:观察长方体的棱(1)一个长方体如图,和AA′平行的棱有多少条?和AB平行的棱有多少条?请用符号把它们表示出来。(2)在同一平面内,任意两条不同的直线有几种位置关系?试着画一画。结论:在同一平面内,两条直线的位置关系只有相交和平行两种。3、如下图,(1)过点B画直线a的平行线,能画出几条?(2)再过点C画直线a的平行线,又能画出几条?此时,两条直线b、c和已知直线a有怎样的位置关系?尝试总结画平行线的步骤,猜想结论。步骤:一放,二靠,三推,四画,五写。结论:平行公理:经过直线外一点,有且只有一条直线与这条直线平行。BDECAFaBCbc注意:点在直线外.....与已知直线平行的直线有无数条。...............讨论:如图:AB∥EF,CD∥EF,直线AB与CD相交吗?为什么?平行线的传递性平行公理的推论:如果两条直线都与第三条直线平行,那么这两条直线也互相平行。(简单说成:平行于同一条直线的两直线平行。)符号语言: a∥b,b∥c∴a∥c设计意图:这个环节主要体现出学生的学,给出问题让学生边看书边思考问题,从而让每位学生都投入紧张的学习中,培养学生的自学能力。三、随堂练习1.如图所示,AB∥CD,EF与AB,CD相交,EF与AB交于点_____,?EF与CD交于______.2.下列说法不正确的是()A.过马路的斑马线是平行线B.100米跑道的跑道线是平行线C.若a∥b,b∥d,则a⊥dD.过直线外一点有且只有一条直线与已知直线平行3.下列说法正确的是()A.同一平面内不相交的两线段必平行B.同一平面内不相交的两射线必平行C.同一平面内不相交的一条线段与一条直线必平行D.同一平面内不相交的两条直线必平行4.如图所示,在这些四边形AB不平行于CD的是()设计意图:发挥学生的主体意识,培养学生的归纳能力。四、拓展延伸1、a、b、c为同一平面内任意三条直线,交点可能有()A.1个或2个或3个B.0个或1个或2个或3个C.1个或2个D.都不对2、利用直尺画图:(1)利用图1中的网格,过P点画直线AB的平行线和垂线(2)把图2网格中的三条线段通过平移使三条线段AB、CD、EF首尾顺次相接组成一个三角形(3)在图3的网格中画一个四边形,满足:①两组对边互相平行;②任意两个顶点都不在一条网格线上③四个顶点都在格点上设计意图:学生可以根据自己的不同水平来巩固自己学过的知识,通过拓展训练,让学生有一定的成就感。五、课堂小结1.平行线的概念:同一平面内,不相交的两条直线叫做平行线。2.平行线的表示:a∥b3.探究同一平面内两条直线的位置关系问题:在同一平面内,两直线的位置关系只有两种:相交和平行。4.平行公理:经过直线外一点,有且只有一条直线与这条直线平行。5.平行公理的推论:平行于同一条直线的两直线平行。设计意图:回顾学过的知识...