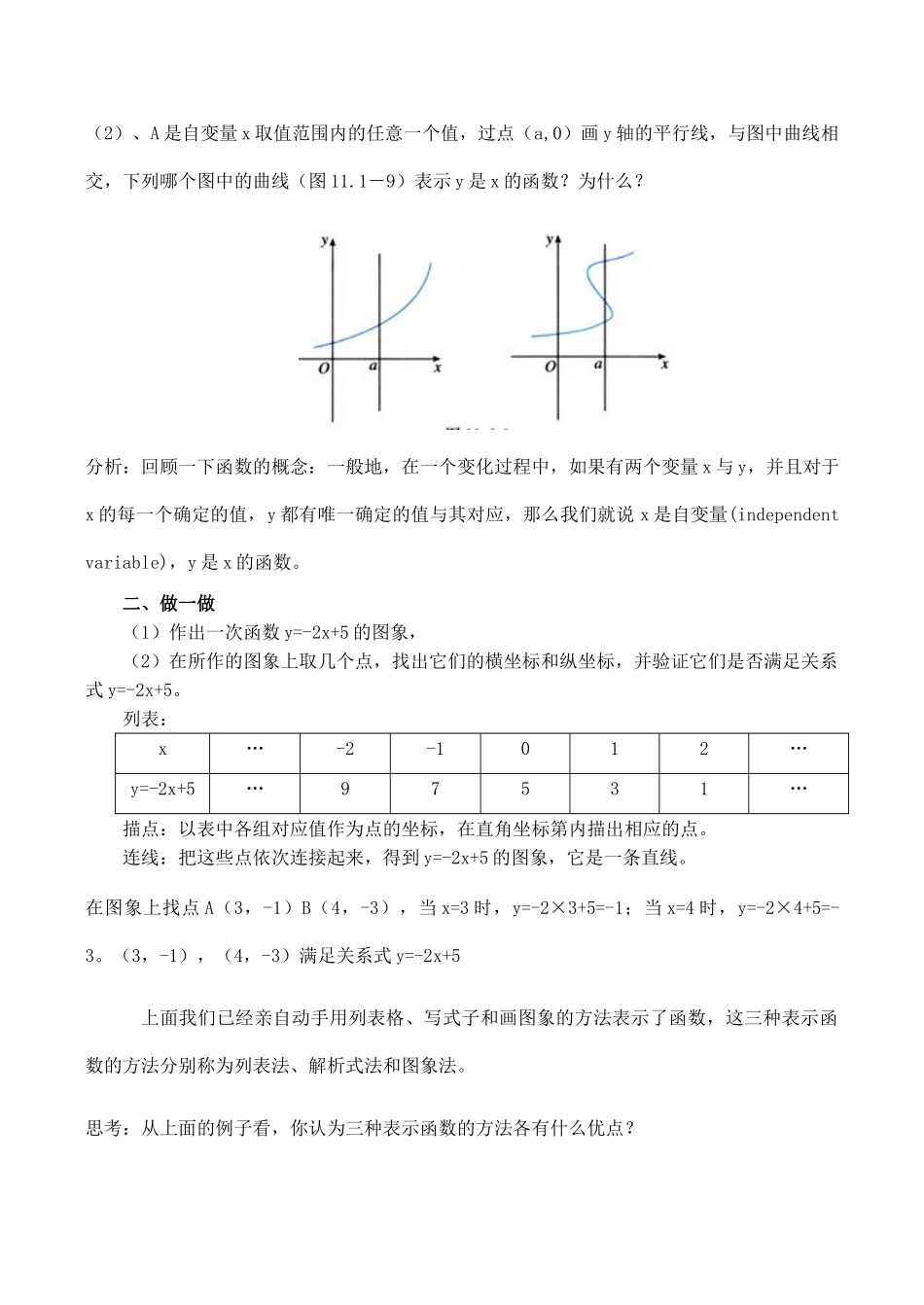
函数的图像第二课时【知识目标】1、在函数的三种表示方法中,会选用适当方法表示函数。2、结合实例,体会“变化与对应”的思想,进一步提高学生利用图象数形结合地分析简单的函数关系的能力.【能力目标】以探索实际问题中的数量关系和变化规律为背景,经历“找出常量和变量,建立并表示函数【情感目标】经历“讨论函数模型、解决实际问题”的过程,体会函数是刻画现实世界中变化规律的重要数学模型。教学重点:进一步理解函数的三种表示方法,并能在实际问题中灵活运用.教学难点:利用所学知识解决相关实际问题。教学过程:一、思考:(1)、下图是一种古代计时器——“漏壶”的示意图,在壶内盛一定量的水,水从壶下的小孔漏出,壶壁内画出刻度,人们根据壶中水面的位置计算时间,用x表示时间,y表示壶底到水面的高度,下面的哪个图象适合表示一小段时间内y与x的函数关系(暂不考虑水量变化对压力的影响)?分析:水向外流的速度是一定的,“漏壶”上下一样,所以,壶底到水面的高度是匀速减小的。(2)、A是自变量x取值范围内的任意一个值,过点(a,0)画y轴的平行线,与图中曲线相交,下列哪个图中的曲线(图11.1-9)表示y是x的函数?为什么?分析:回顾一下函数的概念:一般地,在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是自变量(independentvariable),y是x的函数。二、做一做(1)作出一次函数y=-2x+5的图象,(2)在所作的图象上取几个点,找出它们的横坐标和纵坐标,并验证它们是否满足关系式y=-2x+5。列表:x…-2-1012…y=-2x+5…97531…描点:以表中各组对应值作为点的坐标,在直角坐标第内描出相应的点。连线:把这些点依次连接起来,得到y=-2x+5的图象,它是一条直线。在图象上找点A(3,-1)B(4,-3),当x=3时,y=-2×3+5=-1;当x=4时,y=-2×4+5=-3。(3,-1),(4,-3)满足关系式y=-2x+5上面我们已经亲自动手用列表格、写式子和画图象的方法表示了函数,这三种表示函数的方法分别称为列表法、解析式法和图象法。思考:从上面的例子看,你认为三种表示函数的方法各有什么优点?指导学生深入的思考。表示函数时,要根据具体情况选择适当的方法,有时为全面地认识问题,需要几种方法同时使用。三、学以致用:一水库水位在最近5小时内持续上涨,下表记录了这5小时的水位高度。T/小时0123455Y/千米1010.0510.110.1510.210.25(1)由记录表推出这5小时中水位高度y(单位:米)随时间t(单位:时)变化的函数解析式,并画出函数图象;(2)据估计这种上涨的情况还会持续2小时,预测再过2小时水位高度将达到多少米?分析:记录表已经通过6组数值反映了时间t与水位y之间的对应关系,我们现在需要从这些数值找出这两个变量之间的一般联系规律,由它写出函数解析式,画出函数图象,进而预测水位。解(1)由表中观察到开始水位高10米,以后每隔1小时,水位升高0.05米,这样的变化规律可以表示为y=0.05t+10(0≤t≤7)这个函数的图象如右下图所示:(3)再这2小时的水位高度,就是t=5+2=7,y=0.05t+10的函数值,从解析式容易算出y=0.05×7+10=10.35从函数图象也以估出这个值。2小时后,预计水位高10.35米。归纳:由例4可以看出函数的不同表示法之间可以转化。这充分说明:表示函数时,要根据具体情况选择适当的方法,有时为全面地认识问题,需要几种方法同时使用。四、小结你学习这一节有什么感悟?五:课堂小测试:(每题15分,共60分)1、解析式法与图象法表示等边三角形的周长l是边长a的函数。2、下列式子中的y是x的函数吗?为什么?请再举出一些函数的例子(1)y=3x-5;(2)y=(x-2)/(x-1);(3)3、王教授和孙子小强经常一起进行早锻炼,主要活动是爬山.有一天,小强让爷爷先上,然后追赶爷爷;右图中两条线段分别表示小强和爷爷离开山脚的距离(米)与爬山所用时间(分)的关系(从小强开始爬山时计时),看图回答下列问题:(1)小强让爷爷先上多少米?(2)山顶距离山脚多少米?谁先爬上山顶?(3)小强通过多少时间追上爷爷?4、如图表示某学校秋游活动时,学生乘坐旅游车所行走的路程与时间的关系的示意图,请根...